Question

The tangent at the point P \[\left( {{x_1},{y_1}} \right)\]to the parabola \[{y^2} = 4ax\] meets the parabola \[{y^2} = 4a\left( {x + b} \right)\] at Q and R. the coordinates of the midpoint of QR are
A. \[({x_1} + b,{y_1} + b)\]
B. \[({x_1} - b,{y_1} - b)\]
C. \[({x_1},{y_1})\]
D. \[({x_1} + b,{y_1})\]

Answer 1

Hint:
Here we plot the graph of two parabolas to get a rough idea about the question.

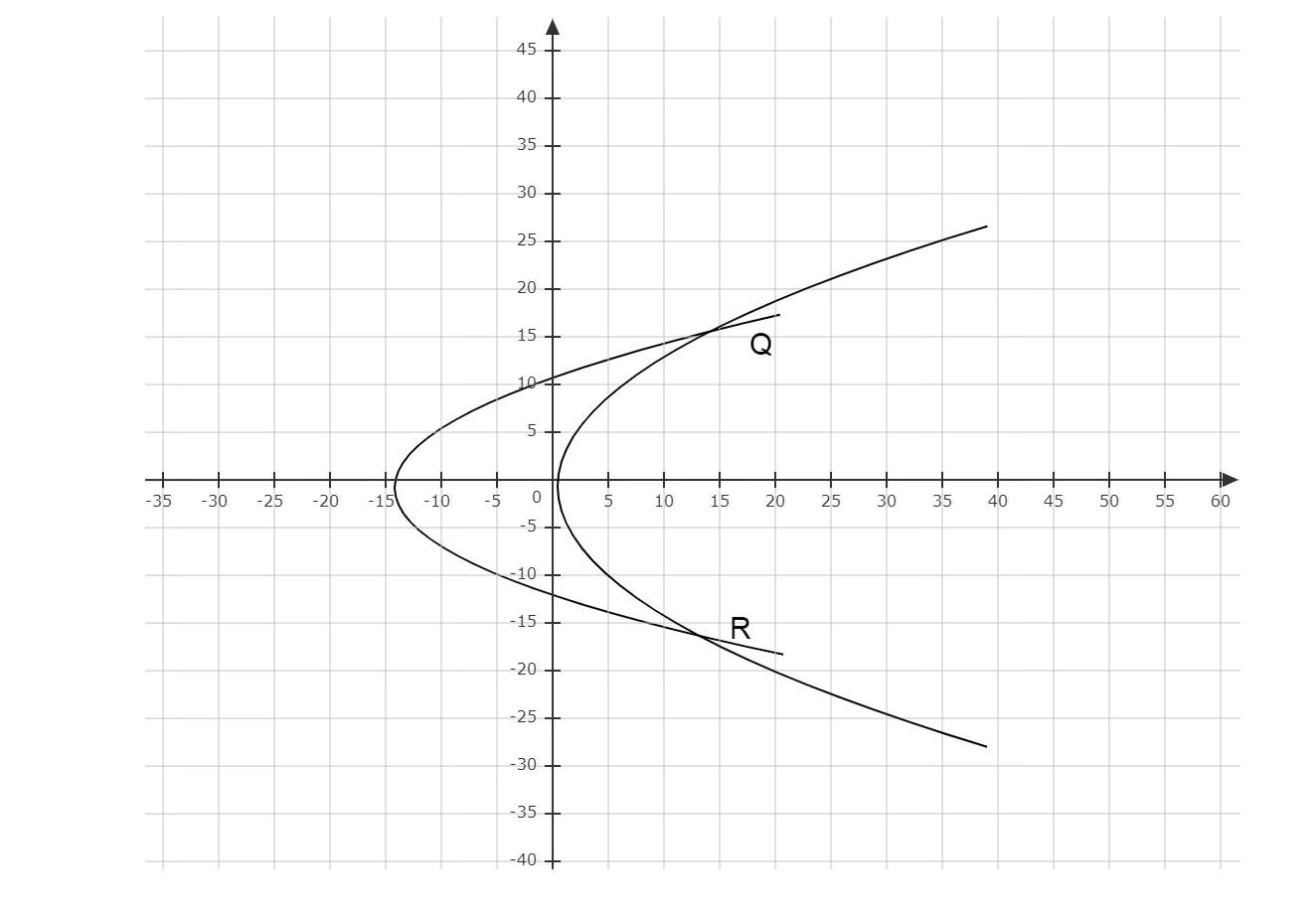
Complete step by step solution:
The equation of the tangent of parabola \[{y^2} = 4ax\] at any point P \[\left( {h,k} \right)\] is given by \[ky = 2a\left( {x + h} \right)\]
Let \[\left( {p,q} \right)\]be the midpoint of the chord
Given, the tangent at the point P \[\left( {{x_1},{y_1}} \right)\] to the parabola \[{y^2} = 4ax\]meets the parabola \[{y^2} = 4a\left( {x + b} \right)\]at Q and R.
Find the equation of the tangent of the parabola by substituting \[{y_1}\]for \[k\]and \[{x_1}\] for \[h\] in \[ky = 2a\left( {x + h} \right)\].
Equation of the tangent is given by \[y{y_1} = 2a\left( {x + {x_1}} \right)\].
\[y{y_1} - 2ax - 2a{x_1} = 0 \ldots \left( 1 \right)\]
The equation of chord with midpoint \[\left( {p,q} \right)\]is given by \[qy - 2a\left( {x + p} \right) - 4ab = {q^2} - 4a\left( {q + b} \right)\].
\[ - 2ax + qy + 2ah - {q^2} = 0 \ldots \left( 2 \right)\]
The tangent and the chord are the same line therefore equation (1) and (2) are the same. Compare both the equations.
\[\dfrac{{2a}}{{ - 2a}} = \dfrac{{ - {y_1}}}{q} = \dfrac{{2a{x_1}}}{{2ap - {q^2}}}\]
This implies that \[{y_1} = q\] and \[2a{x_1} = {q^2} - 2ap\]
Substitute \[{y_1}\]for \[q\]
\[2a{x_1} = {y_1}^2 - 2ap\]
Substitute \[4a{x_1}\] for \[{y_1}^2\] and solve to obtain the value of \[p\]
\[
  2a{x_1} = 4a{x_1} - 2ap \\
  {x_1} = p \\
 \]

Therefore, the midpoint of QR is \[\left( {{x_1},{y_1}} \right)\].

Therefore, Option C is correct.

Note:
In these types of questions, the knowledge of the equation of tangent and chord is very important. And the substitution of points should be done carefully. Students should know equation of parabola \[{y^2} = 4ax\] has centre \[(0,0)\] and equation of parabola \[{y^2} = 4a\left( {x + b} \right)\] has centre \[( - b,0)\].
* Students are recommended to map the graph for better understanding of the question as it helps to find out the tangent, slope of the tangent, chord, normal and slope of the normal.
* A tangent is a straight line that just touches a point on a curve but never cuts the curve.
Equation of tangent of a parabola \[{y^2} = 4ax\] is given by \[{y_1}y = 2a(x + {x_1})\].
* A chord is a straight line segment joining any two points on a curve.
Equation of chord with midpoint \[\left( {p,q} \right)\] is given by \[qy - 2a\left( {x + p} \right) - 4ab = {q^2} - 4a\left( {q + b} \right)\].