Question

The tangent at the point \[\left( {4\cos \phi ,\dfrac{{16}}{{\sqrt {11} }}\sin \phi } \right)\] to the ellipse \[16{x^2} + 11{y^2} = 256\] is also a tangent to the circle \[{x^2} + {y^2} - 2x = 15\]. Find the absolute value of \[\phi \] in degrees.

Answer 1

Hint:
Here we will first find the equation of the tangent. Then we will find the distance of the tangent from the centre of the circle and equate it with the radius of the circle. Further, we will find the value of \[\cos \phi \] in this process and hence, the value of \[\phi \].

Formulas used:
We will use the following formulas:
The tangent to an ellipse with equation \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1{\rm{ }}\] at the point \[\left( {{x_1},{y_1}} \right)\] is given by \[\dfrac{{x{x_1}}}{{{a^2}}} + \dfrac{{y{y_1}}}{{{b^2}}} = 1\].
The distance of a point \[\left( {{x_1},{y_1}} \right)\] from a line \[ax + by + c = 0\] is given by \[d = \dfrac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\].

Complete step by step solution:

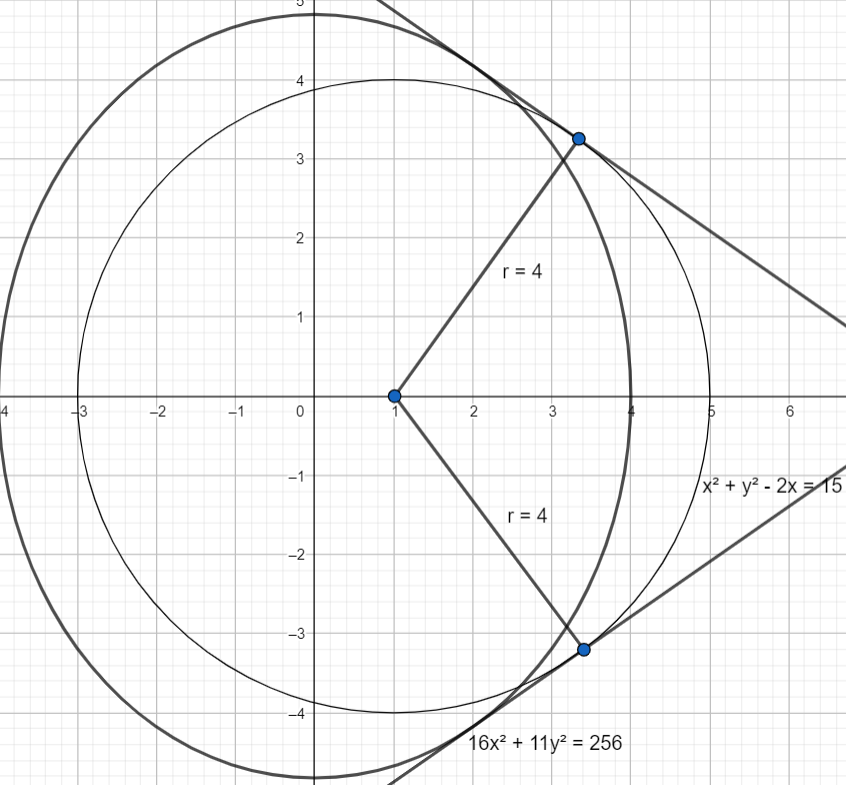
We will write the equation of the ellipse in standard form, \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1{\rm{ }}\]. We will divide both sides of the equation of ellipse by 256. Therefore, we get
\[\begin{array}{l} \Rightarrow \dfrac{{16{x^2}}}{{256}} + \dfrac{{11{y^2}}}{{256}} = \dfrac{{256}}{{256}}\\ \Rightarrow \dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{256/11}} = 1\end{array}\]
Comparing the above equation with \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1{\rm{ }}\], we get
\[a = 4\]
\[b = \dfrac{{16}}{{\sqrt {11} }}\]
The standard form of a circle with centre \[\left( {h,k} \right)\] and radius \[r\] is given by \[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\].
We will convert the equation of the circle given in the question to standard form. We will add and subtract 1 on the left-hand side of the equation and rearrange the terms, So, we get
\[\begin{array}{l} \Rightarrow {x^2} + {y^2} - 2x + 1 - 1 = 15\\ \Rightarrow {x^2} - 2x + 1 + {y^2} - 1 = 15\end{array}\]
Simplifying the expression, we get
\[ \Rightarrow {\left( {x - 1} \right)^2} + {y^2} = 16\]
Rewriting the above equation in standard form, we get
\[ \Rightarrow {\left( {x - 1} \right)^2} + {\left( {y - 0} \right)^2} = {4^2}\]……………………\[\left( 1 \right)\]
We will compare the above equation with \[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\] and find the centre and radius of the circle. So,
\[\begin{array}{l}\left( {h,k} \right) = \left( {1,0} \right)\\r = 4\end{array}\]
We will find the equation of the tangent to the ellipse at point \[\left( {4\cos \phi ,\dfrac{{16}}{{\sqrt {11} }}\sin \phi } \right)\] by substituting \[4\cos \phi \] for \[{x_1}\], \[\dfrac{{16}}{{\sqrt {11} }}\sin \phi \] for \[{y_1}\], 4 for \[a\] and \[\dfrac{{16}}{{\sqrt {11} }}\] for \[b\] in the formula \[\dfrac{{x{x_1}}}{{{a^2}}} + \dfrac{{y{y_1}}}{{{b^2}}} = 1\]. So, we get
\[\begin{array}{l} \Rightarrow \dfrac{x}{{16}} \cdot 4\cos \phi + \dfrac{y}{{11/256}}\dfrac{{16}}{{\sqrt {11} }}\sin \phi = 1\\ \Rightarrow \dfrac{x}{4}\cos \phi + \dfrac{{\sqrt {11} }}{{16}}y\sin \phi = 1\end{array}\]
Simplifying the above equation, we get
\[ \Rightarrow 4x\cos \phi + \sqrt {11} y\sin \phi = 16\]……………………………..\[\left( 2 \right)\]
The above line is also a tangent to the circle \[{x^2} + {y^2} - 2x = 15\].
We know that the distance between the centre of a circle and the point of contact of a tangent is the same as the length of the radius of the circle. We will use this property; we will substitute 4 for \[d\], \[4\cos \phi \] for \[a\] ,\[\sqrt {11} \sin \phi \] for \[b\], \[ - 1\] for \[c\], 1 for \[{x_1}\] and 0 for \[{y_1}\] in the formula \[d = \dfrac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\].
Therefore we get
\[ \Rightarrow 4 = \dfrac{{\left| {4\cos \phi - 16} \right|}}{{\sqrt {16{{\cos }^2}\phi + 11{{\sin }^2}\phi } }}\]
On cross multiplication, we get
\[\begin{array}{l} \Rightarrow 16{\cos ^2}\phi + 11{\sin ^2}\phi = {\left( {\cos \phi - 4} \right)^2}\\ \Rightarrow 16{\cos ^2}\phi + 11{\sin ^2}\phi = {\cos ^2}\phi + 16 - 8\cos \phi \end{array}\]
Adding and subtracting the like terms, we get
\[\begin{array}{l} \Rightarrow 15{\cos ^2}\phi + 11\left( {1 - {{\cos }^2}\phi } \right) + 8\cos \phi - 16 = 0\\ \Rightarrow 4{\cos ^2}\phi + 8\cos \phi - 5 = 0\end{array}\]
Now factoring the above equation, we get
\[ \Rightarrow \left( {2\cos \phi + 5} \right)\left( {2\cos \phi - 1} \right) = 0\]
Using zero product property, we get
\[\begin{array}{l} \Rightarrow \left( {2\cos \phi + 5} \right) = 0\\ \Rightarrow \cos \phi = - \dfrac{5}{2}\end{array}\]
or
\[\begin{array}{l} \Rightarrow \left( {2\cos \phi - 1} \right) = 0\\ \Rightarrow \cos \phi = \dfrac{1}{2}\end{array}\]
\[\cos \phi \] cannot be \[ - \dfrac{5}{2}\] as the minimum value of the function is \[ - 1\]. So \[\cos \phi \] will be \[\dfrac{1}{2}\].
We know that \[\cos 60^\circ = \dfrac{1}{2}\].

therefore, the absolute value of \[\phi \] is 60 degrees.

Note:
As \[\cos \phi = \dfrac{1}{2}\], \[\phi \] can be both \[60^\circ \] or \[ - 60^\circ \], so there will be 2 tangents that are common to the circle and the ellipse. One of them will have a positive slope and the other will have a negative slope. The concept of tangents is used to find the instantaneous rate of change of a function.
We have used the zero product property to simplify the equation. Zero product property states that if \[a \cdot b = 0\], then either \[a = 0\] or \[b = 0\].