Question

The sun is ${{60^\circ }}$ above the horizon. A ray of sunlight on refraction at a surface of water (refractive index, 4/3) will suffer a deviation of-
A. ${{60^\circ - si}}{{{n}}^{{{ - 1}}}}\left( {\dfrac{{{3}}}{{{8}}}}
\right)$
B. ${{30^\circ - si}}{{{n}}^{{{ - 1}}}}\left( {\dfrac{{{{3}}\sqrt {{3}}
}}{{{8}}}} \right)$
C. ${{30^\circ - si}}{{{n}}^{{{ - 1}}}}\left( {\dfrac{{{3}}}{{{8}}}}
\right)$
D. ${{60^\circ - si}}{{{n}}^{{{ - 1}}}}\left( {\dfrac{{{{3}}\sqrt {{3}}
}}{{{8}}}} \right)$

Answer 1

Hint: As value of refractive index is given in this question, ${{\mu = }}\dfrac{{{4}}}{{{3}}}$ . For finding the deviation of ray of sunlight on a surface of water, firstly consider one right angle triangle by considering that the sun is ${{60^\circ }}$above the horizon. After finding the sides of a triangle, we can easily find out the value of all angles of triangles. We will get two equations, by comparing those two we can easily find the deviation.

Complete step by step solution:
Given: the sun is ${{60^\circ }}$above the horizon.
${{\mu = }}\dfrac{{{4}}}{{{3}}}$
Since the sun is ${{60^\circ }}$above the horizon, we can draw a right angled triangle and consider the base of the triangle is horizon whereas the hypotenuse of the triangle and the horizon is making angle of ${{60^\circ }}$ represents the sun is ${{60^\circ }}$ above the horizon,
In the following diagram A is sun, BC is horizon.

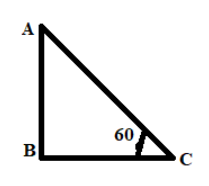
Hence when a ray of sunlight enters into water, the refraction at a surface water takes place. Where the refractive index of water is $\dfrac{{{4}}}{{{3}}}$
Hence ,$\dfrac{{{1}}}{{{\mu }}}{{ = }}\dfrac{{{3}}}{{{4}}}$ ………(I)
Since there is total refraction takes place at the surface of the water,
${{d = }}\dfrac{{{1}}}{{{{2\mu }}}}{{ = }}\dfrac{{{3}}}{{{8}}}$
Now if we consider AB = 4 and BC = 3 according to pythagoras theorem,
${{AC = }}\sqrt {{{{{(AB)}}}^{^{{2}}}}{{ + (BC}}{{{)}}^{{2}}}} $
${{AC = }}\sqrt {{{{{(4)}}}^{^{{2}}}}{{ + (3}}{{{)}}^{{2}}}} {{ = 5}}$
Since sum of all angles of a triangle is equals to ${{180^\circ }}$,
If \[\angle {{C = 60^\circ }}\] and $\angle {{B = 90^\circ }}$then $\angle {{A = 30^\circ }}$
\[{{Sin 30^\circ = }}\dfrac{{{{BC}}}}{{{{AB}}}}\]
\[\therefore {{Sin 30^\circ = }}\dfrac{{{3}}}{{{4}}}\] ……………….(II)
Now from equation (I) and (II),
$\dfrac{{{1}}}{{{\mu }}}{{ = sin30^\circ }}$
$\therefore {{\mu = }}\dfrac{{{1}}}{{{{sin30^\circ }}}}$
${{d = 30^\circ - si}}{{{n}}^{{{ - 1}}}}{{(}}\dfrac{{{3}}}{{{8}}}{{)}}$

Hence option (C) is the correct answer.

Note: It must be noted that while taking the angles in a triangle care should be taken that for what angle we are taking sin and cos must be the corresponding one only. The Pythagorean theorem consists of a formula ${{{x}}^{{2}}}{{ + }}{{{y}}^{{2}}}{{ = }}{{{z}}^{{2}}}$ which is used to figure out the value of (mostly) the hypotenuse side in a right angled triangle. The $x$ and$y$ are the $2$ "non-hypotenuse" sides of the triangle (Opposite side and Adjacent side), and z is the hypotenuse side opposite to right angle.