Question

The straight line $2x - 3y = 1$ divides the circular region ${x^2} + {y^2} \leqslant 6$ into two parts. If $S = \left\{ {\left( {2,\dfrac{3}{4}} \right),\left( {\dfrac{5}{2},\dfrac{3}{4}} \right),\left( {\dfrac{1}{4}, - \dfrac{1}{4}} \right),\left( {\dfrac{1}{8},\dfrac{1}{4}} \right)} \right\}$ ,then the numbers of points in $S$ lying inside the smaller part is
A) 1
B) 2
C) 3
D) 4

Answer 1

Hint: For each point first check if it is inside the circular region or not, for this find the distance of that point from the centre of the circle using distance formula. If a point lies inside, we check if the point lies below or above the given line and also check if the smaller part is below or above the line. A point $(x,y)$ lies below the line if $ax + by + c < 0$ and above the line if $ax + by + c > 0$.

Complete step-by-step answer:
Given line $2x - 3y = 1$ and circle is ${x^2} + {y^2} \leqslant 6$ are represented in the graph below.

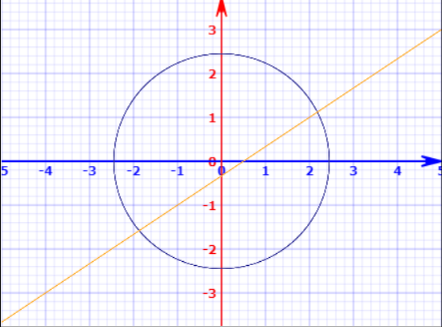
As shown in the graph, the smaller part is the circular region below the given line.
A point $(x,y)$is inside the graph if ${x^2} + {y^2} < 6$ (to check point is inside the given circular region) and $2x - 3y - 1 > 0$ (to check point is below the given line).
For point $\left( {2,\dfrac{3}{4}} \right)$ , ${2^2} + {\left( {\dfrac{3}{4}} \right)^2} < 6$ then point lies inside the circle and $2.2 - 3.\dfrac{3}{4} - 1 = 3 - \dfrac{9}{4} = \dfrac{3}{4} > 0$ then point lies inside the smaller part.
For point $\left( {\dfrac{5}{2},\dfrac{3}{4}} \right)$ , ${\left( {\dfrac{5}{2}} \right)^2} + {\left( {\dfrac{3}{4}} \right)^2} > 6$ then point lies outside the circle, then this point is not lies inside the smaller part.
For point $\left( {\dfrac{1}{4}, - \dfrac{1}{4}} \right)$ , ${\left( {\dfrac{1}{4}} \right)^2} + {\left( { - \dfrac{1}{4}} \right)^2} < 6$ then point lies inside the circle and $\dfrac{2}{4} + \dfrac{3}{4} - 1 = \dfrac{1}{4} > 0$ then point lies inside the small part.
For point $\left( {\dfrac{1}{8},\dfrac{1}{4}} \right)$ , ${\left( {\dfrac{1}{8}} \right)^2} + {\left( {\dfrac{1}{4}} \right)^2} < 6$ then point lies inside the circle and $\dfrac{2}{8} - \dfrac{3}{4} - 1 < 0$ then point lies inside the larger part not in smaller part.
Hence points $\left( {\dfrac{1}{4}, - \dfrac{1}{4}} \right)$ and $\left( {2,\dfrac{3}{4}} \right)$ are two points lies inside the smaller part.

Hence, correct answer is option B.

Note: In some cases, a point may lie on the boundary of the region, don't count that point. If a point lies outside the circle, simply cancel that point; we don’t check its position with respect to the line as done for the second point. For a shorter method, mark all points on the graph then check manually if it lies inside the smaller part or not.