Question

The Square on the diagonal of a cube has an area of $1875c{{m}^{2}}$ .Calculate:
i)The side of the cube,
ii)The total surface area of the cube.

Answer 1

Hint: Diagonal of a cube is $a\sqrt{3}$ , where a is the side of any cube and area of the square can be given by formula $\text{side}\times \text{side}$ . Use these two formulae to solve the problem. Here, the diagonal of the cube is the side of the square.

Complete Complete step by step answer:

Let the side of the diagonal be ‘x’ cm. Now, it is given that the area of the square formed on the diagonal of the cube (diagonal is acting as a side of square) is $1875c{{m}^{2}}$ . So, diagram can be given as

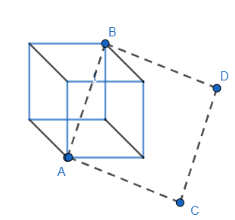
Here AB is the diagonal of the cube and ABCD is the square whose area is $1875c{{m}^{2}}$ .
So, we know that the area of the square is $\text{side}\times \text{side}$ . Hence, area of square ABCD can be given as $AB\times AB={{\left( AB \right)}^{2}}$ . so we get
$\begin{align}
  & {{\left( AB \right)}^{2}}=1875=3\times 25\times 25 \\
 & AB=\sqrt{3\times 25\times 25} \\
 & AB=25\sqrt{3}cm. \\
\end{align}$
Now, we know the length of the diagonal of a cube with side ‘a’ can be given as $a\sqrt{3}$ . Hence, we have a side of length x cm and diagonal of length $25\sqrt{3}\left( AB \right)$ . Hence, we can write
$x\sqrt{3}=25\sqrt{3}$
x = 25 cm.
Hence, the side of the cube is 25 cm.
 ii) Here, we have to determine the total surface area of the cube. It is given the area of the cube. It is given with respect to side ‘a’ as
Total surface area of a cube $=6{{a}^{2}}$
So, we have already calculated the length of the side of the cube as 25m. Hence, we can get total surface area of the cube as
Total surface area of given cube,
$\begin{align}
  & =6{{x}^{2}} \\
 & =6\times {{25}^{2}} \\
 & =6\times 625 \\
 & =3750c{{m}^{2}} \\
\end{align}$
Hence, the total surface area of the cube is $3750c{{m}^{2}}$ .

Note: One may prove the diagonal length of cube as,

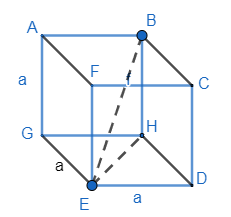
Apply Pythagoras in $\Delta HED$ in the square of the base part. So, we get
$\begin{align}
  & E{{H}^{2}}={{a}^{2}}+{{a}^{2}}=2{{a}^{2}} \\
 & EH=\sqrt{2a} \\
\end{align}$
Now, in $\Delta EHB$ , we get
$\begin{align}
  & E{{B}^{2}}=E{{H}^{2}}+H{{B}^{2}} \\
 & E{{B}^{2}}=2{{a}^{2}}+{{a}^{2}}=3{{a}^{2}} \\
 & EB=\sqrt{3}a \\
\end{align}$
One may get confused with the total surface area and lateral surface area. Total surface area means we need to include all six faces and lateral means we need to have upper and lower faces from the total surface area $\left( 4{{a}^{2}} \right)$ , so we clear with the terminology part as well. Diagonal of the cube is acting as a side of the square not as the diagonal of any square. In other words, the diagonal of a cube is not the diagonal of any square in the problem. So, be clear with the words as well.