Question

The solution set of ${\left( x \right)^2} + {\left( {x + 1} \right)^2} = 25$ , where (x) denotes the nearest integer greater or equal to x is
A. [-4,3)$ \cup $ [3,4)
B. (-5,-4] $ \cup $ (2,3]
C. (2,4)
D. None of these

Answer 1

Hint: First we’ll assume (x) with an integer variable, then we’ll get a quadratic equation in that variable, on solving that equation we’ll have its value. With the help of those solutions, we’ll conclude the interval of x as obtaining the solution of those equations will give us the value of (x) but we have to find the value of x.

Complete step by step answer:

Given data: ${\left( x \right)^2} + {\left( {x + 1} \right)^2} = 25..............(i)$
Now, it is given that (x) is the least integer function that gives only integer value.
Let $\left( x \right) = t$, where t is an integer.
Therefore, $\left( {x + 1} \right) = t + 1$
Now, substituting the value of ${\left( x \right)^2}$and ${\left( {x + 1} \right)^2}$in equation(i),
i.e. ${t^2} + {\left( {t + 1} \right)^2} = 25$
On expanding the square term,
$ \Rightarrow {t^2} + {t^2} + 1 + 2t = 25$
$ \Rightarrow {t^2} + {t^2} + 1 + 2t - 25 = 0$
Solving for the like terms
$ \Rightarrow 2{t^2} + 2t - 24 = 0$
Dividing the whole equation by 2
$ \Rightarrow {t^2} + t - 12 = 0$
Now, splitting the coefficient of t such that they will be factors of ${t^2}$and the constant term
$ \Rightarrow {t^2} + (4 - 3)t - 12 = 0$
Now, simplifying the brackets,
$ \Rightarrow {t^2} + 4t - 3t - 12 = 0$
Taking common from the first two and last two terms,
$ \Rightarrow t(t + 4) - 3(t + 4) = 0$
Taking (t+4) common from both the terms,
$ \Rightarrow (t + 4)(t - 3) = 0$
i.e. $t + 4 = 0$ or $t - 3 = 0$
Therefore, $t = - 4$ or $t = 3$
When $t = - 4$
i.e. $(x) = - 4$
since (x) is the integer greater or equal to x
$\therefore x \in ( - 5, - 4]$
Similarly, when $t = 3$
i.e. $(x) = 3$
$\therefore x \in (2,3]$
Combining the values of x, we get
That $x \in ( - 5, - 4] \cup (2,3]$
Option(B) is correct

Note: In the given solution we’ve talked about the least integer function (x). let us draw a graph of the least integer function for a better understanding of this function.

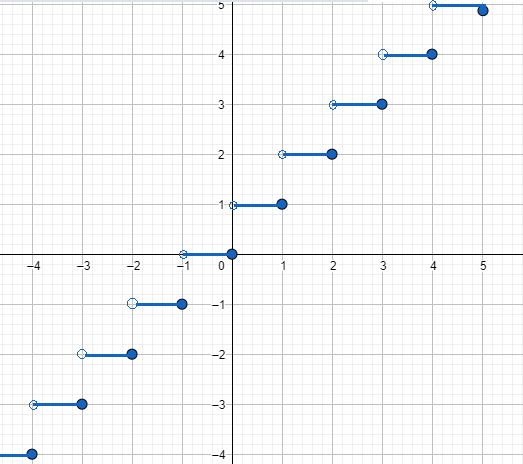
So from the graph, we can say that if the value of $x \in (2,3]$ then the value of (x) (denotes the nearest integer greater or equal to x) is 3.