Question

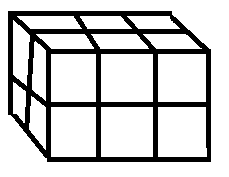
The solid brick shown is made of small bricks of the side \[1\] unit. When the large brick is disassembled into its component small bricks, the total surface area of the small bricks is how much greater than the surface area of the large brick?

Answer 1

Hint: In the given question, we are a large brick made up by stacking several small bricks together. So, the dimensions of the small bricks are given to us. We can find the dimensions of the large brick by counting the number of small cube bricks in the length and breadth of the larger cuboidal brick. Then, we find the total surface area of the small brick as well as the large brick and compare both of them.

Complete step by step solution:
So, the side of the small cube bricks is given to us as \[1\] unit.
Now, the number of small cube bricks in length, breadth and height of cuboidal brick is $3$, $2$ and $2$ respectively.
Hence, the number of small bricks constituted in the large brick is $3 \times 2 \times 2 = 12$.
Now, we know that the formula for the total surface area of a cube is $6 \times {\left( {Side} \right)^2}$.
Now, we know that the side of the small cube bricks is \[1\] unit.
So, the total surface area of the small brick is $6 \times {\left( 1 \right)^2} = 6$ square units.
Also, there are a total of $12$ such small cube bricks stacked together in the large cuboidal brick.
Hence, the total surface area of $12$ such small cubes is $6 \times 12 = 72$ square units.
Now, we also know that the formula for finding the total surface area of a cuboid is $2\left( {lb + bh + hl} \right)$ where $l, b$ and $h$ represent the length, breadth and height of the cuboid respectively.
So, we know that the length of the large cuboidal brick is $3$ units. The breadth is $2$ units and the height is $2$ units.
So, we get the total surface area of the brick as $2\left( {3 \times 2 + 2 \times 2 + 2 \times 3} \right)$
$ \Rightarrow 2\left( {6 + 4 + 6} \right)$ square units
$ \Rightarrow 2\left( {16} \right)$ square units
$ \Rightarrow 32$ square units
So, we get the total surface area of the smaller bricks as $72$ square units and the total surface area of the large cuboidal brick as $32$ square units.
Hence, the total surface area of the smaller bricks is $40$ square units greater than the total surface area of the large cuboidal brick.

Note:
Generally the area is the region occupied by a thing. One must have a strong grip over the concepts of mensuration in order to solve such types of problems. Care should be taken while handling the calculative steps in order to be sure of the answer.