Question

The slant height of a cone is 13 cm and radius is 5 cm, then its height is-
A) 5 cm
B) 22 cm
C) 12 cm
D) 18 cm

Answer 1

Hint: Use the formula $l = \sqrt {{r^2} + {h^2}} $, where $l = $ slant height of the cone, $r = $ radius of the cone, $h = $height of the cone.

Complete step-by-step answer:

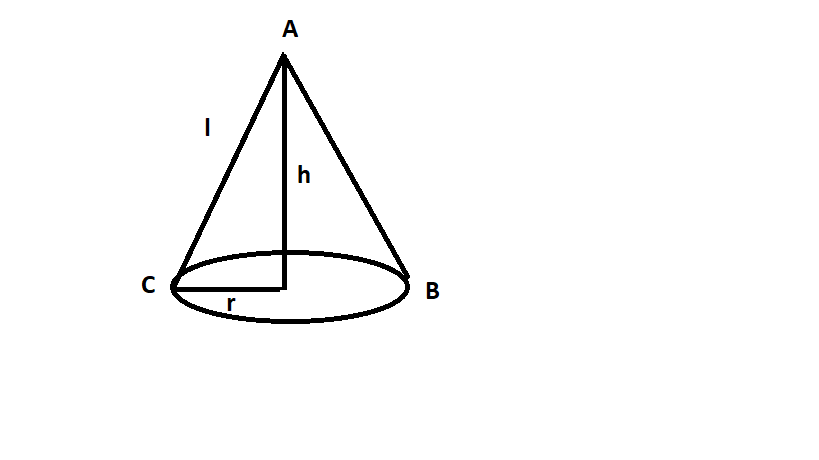
We have been given in the question that-
$l = $ slant height of the cone = 13 cm
$r = $ radius of the cone = 5 cm.
Let us refer to the figure for better understanding, ABC is a cone having l as the slant height, h as the altitude and r as the radius.

Now, using the formula, $l = \sqrt {{r^2} + {h^2}} $, where $l = $ slant height of the cone, $r = $ radius of the cone, $h = $ height of the cone.
$l = \sqrt {{r^2} + {h^2}} $
Squaring both sides-
$
  l = \sqrt {{r^2} + {h^2}} \\
   \Rightarrow {l^2} = {r^2} + {h^2} \\
   \Rightarrow {h^2} = {l^2} - {r^2} \\
   \Rightarrow h = \sqrt {{l^2} - {r^2}} \\
$
Putting the value of $l = 13cm,r = 5cm$, we get-
$h = \sqrt {{{13}^2} - {5^2}} = \sqrt {169 - 25} = \sqrt {144} = 12cm$
Hence, the height of the cone is 12 cm.
So, the correct option is C. 12 cm.

Note: Whenever such types of questions appear, then write the things given in the question. Then, use the standard formula $l = \sqrt {{r^2} + {h^2}} $, and then by squaring both sides, we will get $h = \sqrt {{l^2} - {r^2}} $. Put the values of $l = 13cm,r = 5cm$, and obtain the value of height h of the cone.