Question

The sides of the quadrangular field taken in order are \[26,27,7,24m\] respectively. The angle contained by the last \[2\] sides is a right angle. Find its area.

Answer 1

Hint: Draw the diagram of the quadrangular first and then as given that the quadrangular is divided into two triangles in which one is right angled triangle and another is normal triangle. So, the diagonal of a right angled triangle will be the third side of the normal triangle. So, calculate the third side using Pythagoras theorem as \[\sqrt {A{D^2} + C{D^2}} = AC\]. And then calculate the area of right angle triangle as \[\Delta ADC = \dfrac{1}{2} \times AD \times CD\]and calculate the area of normal triangle using Heron’s formula as \[\Delta ABC = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} ,\] where s is the semi-perimeter of \[\Delta ABC\], as \[s = \dfrac{{a + b + c}}{2}\], and a, b, c are sides of the triangle. Hence, on adding area of both triangles the required answer can be calculated.

Complete step-by-step answer:
As the given sides of the quadrangular field taken in order are \[26,27,7,24m\] respectively.
Diagram:

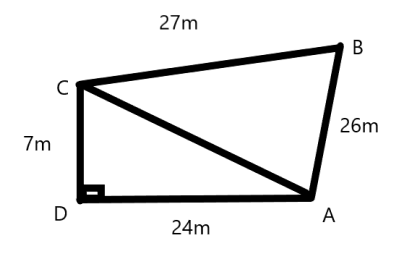
Hence, \[AB = 26m\], \[BC = 27m\], \[CD = 7m\], \[DA = 24m\].
As, \[\Delta ADC\] is a right angled triangle,
So, first apply Pythagoras theorem in order to calculate the length of side AC.
\[ \Rightarrow \]\[\sqrt {A{D^2} + C{D^2}} = AC\]
On substituting the values, we get,
\[ \Rightarrow \]\[\sqrt {{{24}^2} + {7^2}} = AC\]
On expanding the term, we get,
\[ \Rightarrow \]\[\sqrt {576 + 49} = AC\]
Again, on simplifying, we get,
\[ \Rightarrow \]\[\sqrt {625} = AC\]
Hence, we can see that \[\sqrt {{{25}^2}} = AC\]
And the value of AC is \[AC = 25m\].
Hence, calculating the area of \[\Delta ADC\]using the formula of right angled triangle as,
\[\Delta ADC = \dfrac{1}{2} \times AD \times CD\]
Hence, on substituting the values, we get,
\[ \Rightarrow \]\[\Delta ADC = \dfrac{1}{2} \times 24 \times 7\]
Hence, on simplifying further, we get,
\[
   = 12 \times 7 \\
   = 84{m^2} \\
 \]
So, area of \[\Delta ADC\]\[ = 84{m^2}\]
Now, calculating the area of \[\Delta ABC\],
So first calculate the semi-perimeter of \[\Delta ABC\].
\[s = \dfrac{{AB + BC + CA}}{2}\]
Hence, substituting the values of sides, we get,
\[ \Rightarrow \]\[s = \dfrac{{26 + 25 + 27}}{2}\]
On simplifying we get,
\[ \Rightarrow \]\[s = 39m\]
Now, using Heron’s formula to find area of triangle as \[\Delta ABC = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} ,\]
So, on substituting the values in the above equation as
\[ \Rightarrow \]\[\Delta ABC = \sqrt {39\left( {39 - 26} \right)\left( {39 - 27} \right)\left( {39 - 25} \right)} \]
On calculating the above value, we get,
\[ \Rightarrow \]\[\Delta ABC = \sqrt {39\left( {13} \right)\left( {12} \right)\left( {14} \right)} \]
On simplification we get,
\[ \Rightarrow \]\[\Delta ABC = \sqrt {85179} \]
On further calculation we get,
\[ \Rightarrow \]\[\Delta ABC = 291.85{m^2}\]
Hence, on summation or area of both the triangles we get the area of quadrangular as,
\[\Delta ABC + \Delta ADC\]
On substituting the values,
\[ = \left( {84 + 291.85} \right){m^2}\]
On adding, we get,
\[ = 375.85{m^2}\]
The area of quadrangular is \[375.85{m^2}\].

Note: Apply the concept of Pythagoras theorem and Heron’s formula carefully which are given as \[\sqrt {A{D^2} + C{D^2}} = AC\]and \[\Delta ABC = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} ,\]remember that the area of right angle triangle is given as \[\Delta ADC = \dfrac{1}{2} \times AD \times CD\].
Hence, also remember that \[s = \dfrac{{a + b + c}}{2}\]. Thus, calculate properly and hence the above quadrangularis area can be calculated.