Question

The sides of a right-angled triangle containing the right angle are ${\text{5x cm}}$and ${\text{3x - 1 cm}}$. If its area is ${\text{60c}}{{\text{m}}^{\text{2}}}$, find its perimeter.

Answer 1

Hint: Area of a right-angled triangle is given by half the product of its non-hypotenuse sides. Using this relation, we can solve for ${\text{x}}$. Using the Pythagoras theorem, we can find the hypotenuse. Then we get the perimeter by taking the sum of the three sides.

Complete step by step answer:

For easy understanding, we can draw a diagram with the given details

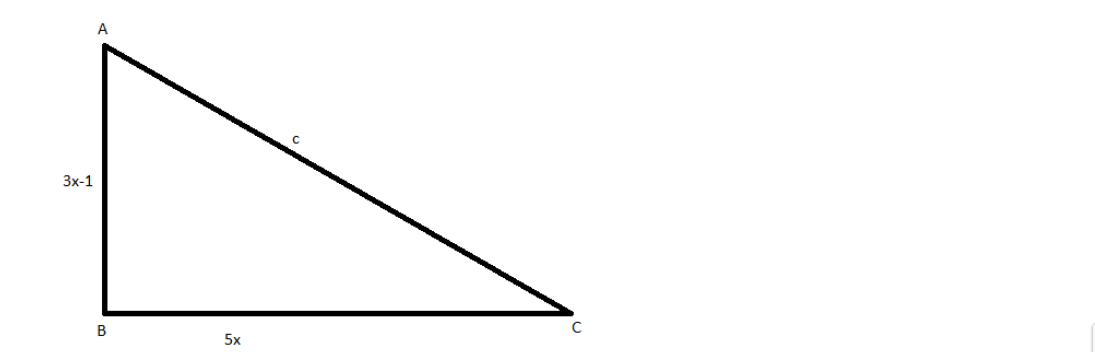
We have $\Delta ABC$ right angled at B. So, its hypotenuse is AC. It is given to us that sides containing the right angle are ${\text{5x cm}}$and ${\text{3x - 1 cm}}$. So, we can take ${\text{BC = 5x cm}}$and ${\text{AB = 3x - 1 cm}}$
Area of the triangle is given by, ${\text{A = }}\dfrac{{\text{1}}}{{\text{2}}}{\text{ $\times$ base $\times$ height}}$
Here base is ${\text{5x cm}}$ and height is ${\text{3x - 1 cm}}$,
On substituting the values, we get,
\[ \Rightarrow \dfrac{{\text{1}}}{{\text{2}}}{\text{ $\times$ }}\left( {{\text{3x - 1}}} \right){\text{ $\times$ 5x = 60}}\]
On simplification, we get,
${\text{15}}{{\text{x}}^{\text{2}}}{\text{ - 5x = 120}}$
$ \Rightarrow {\text{3}}{{\text{x}}^{\text{2}}}{\text{ - x - 24 = 0}}$
On using the formula \[{\text{x = }}\dfrac{{{\text{ - b $\pm$ }}\sqrt {{{\text{b}}^{\text{2}}}{\text{ - 4ac}}} }}{{{\text{2a}}}}\], where \[{\text{a = 3,b = - 1,c = - 24}}\],
We get,
\[
  {\text{x = }}\dfrac{{{\text{ - ( - 1) $\pm$ }}\sqrt {{{{\text{( - 1)}}}^{\text{2}}}{\text{ - 4 $\times$ 3 $\times$ ( - 24)}}} }}{{{\text{2 $\times$ 3}}}} \\
  {\text{ = }}\dfrac{{{\text{1 $\pm$ }}\sqrt {{\text{1 + 288}}} }}{{\text{6}}} \\
  {\text{ = }}\dfrac{{{\text{1 $\pm$ }}\sqrt {{\text{289}}} }}{{\text{6}}} \\
  {\text{ = }}\dfrac{{{\text{1 $\pm$ 17}}}}{{\text{6}}} \\
 \]
Considering \[{\text{x = }}\dfrac{{{\text{1 + 17}}}}{{\text{6}}}\]we get, \[{\text{x = 3}}\]
And on considering, \[{\text{x = }}\dfrac{{{\text{1 - 17}}}}{{\text{6}}}\], we get,
\[{\text{x = }}\dfrac{{{\text{ - 16}}}}{{\text{6}}}{\text{ = }}\dfrac{{{\text{ - 8}}}}{{\text{3}}}\]
Therefore,${\text{x = - }}\dfrac{{\text{8}}}{{\text{3}}}{\text{,3}}$
${\text{x = - }}\dfrac{{\text{8}}}{{\text{3}}}$ is not possible as it cannot be negative.
For ${\text{x = 3}}$,
So, the sides are,
${\text{5x = 5 $\times$ 3 = 15cm}}$
${\text{3x - 1 = 3 $\times$ 3 - 1 = 8 - 1 = 9cm}}$
Using Pythagoras theorem which is \[AC = \sqrt {A{B^2} + B{C^2}} \], the third side is given by,
${\text{c = }}\sqrt {{\text{1}}{{\text{5}}^{\text{2}}}{\text{ + }}{{\text{8}}^{\text{2}}}} {\text{ = }}\sqrt {{\text{225 + 64}}} {\text{ = }}\sqrt {{\text{289}}} {\text{ = 17cm}}$
The perimeter is given by ${\text{P = 15 + 8 + 17 = 40cm}}$
The perimeter of the given triangle is ${\text{40cm.}}$

Note: Drawing diagram is very helpful for understanding the problem. The concepts used here are the area of a triangle, solving quadratic equations, and Pythagoras theorem. We must read the question carefully and take the sides as given in the question. While solving quadratic equations of variable related to length, the negative roots or roots giving negative values for length is rejected. We must not take the negative roots and use its modulus. The quadratic equation we got here cannot be solved by the factorization method. We can also check the discriminant to know the nature of the root.