Question

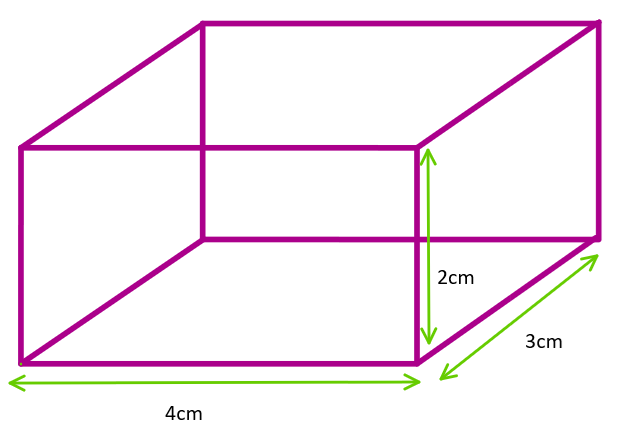
The sides of a rectangular block are 2 cm, 3 cm, and 4 cm. The ratio of maximum to minimum resistance between its parallel faces is:
A. 4
B. 3
C. 2
D. 1

Answer 1

Hint: This is a direct question. We will make use of the formula that relates the resistance of the material with its resistivity, its area, and the length of the material. The maximum resistance of a block has a maximum length and the minimum area, whereas, the minimum resistance of a block has a minimum length and the maximum area. Thus we will divide these values to find the ratio.
Formulae used:
\[R=\dfrac{\rho l}{A}\]

Complete step by step solution:

The formula for computing the resistance of the material is given as follows.
\[R=\dfrac{\rho l}{A}\]
Where R is the resistance of the material, \[\rho \]is the resistivity of the material, l is the length of the material and A is the area of the material.
The maximum resistance of the rectangular block is given as follows.
\[{{R}_{\max }}=\dfrac{\rho {{l}_{\max }}}{{{A}_{\min }}}\]
The minimum resistance of the rectangular block is given as follows.
\[{{R}_{\min }}=\dfrac{\rho {{l}_{\min }}}{{{A}_{\max }}}\]
Now, we will compute the ratio of the maximum to the minimum resistance of the rectangular block. So, we get,
\[\dfrac{{{R}_{\max }}}{{{R}_{\min }}}=\dfrac{\rho {{l}_{\max }}}{{{A}_{\min }}}\times \dfrac{{{A}_{\max }}}{\rho {{l}_{\min }}}\]
The resistivity of the block remains the same.
\[\begin{align}
&\dfrac{{{R}_{\max }}}{{{R}_{\min }}}=\dfrac{\rho {{l}_{\max }}}{{{A}_{\min }}}\times \dfrac{{{A}_{\max }}}{\rho {{l}_{\min }}} \\
 & \dfrac{{{R}_{\max }}}{{{R}_{\min }}}=\dfrac{{{A}_{\max }}\times {{l}_{\max }}}{{{A}_{\min }}\times {{l}_{\min }}} \\
\end{align}\]
From the data, we have the data as follows.
The sides of the rectangle are 2 cm, 3 cm, and 4 cm. Thus, the maximum length will be 4 cm and the maximum area will be \[(4\times 3)\,c{{m}^{2}}\], similarly, the minimum length will be 2 cm and the minimum area will be \[(2\times 3)\,c{{m}^{2}}\].
Substitute these values in the above equation.
\[\begin{align}
  & \dfrac{{{R}_{\max }}}{{{R}_{\min }}}=\dfrac{(4\times 3)\times 4}{(2\times 3)\times 2} \\
 & \dfrac{{{R}_{\max }}}{{{R}_{\min }}}=4 \\
\end{align}\]
$\therefore$ The ratio of maximum to minimum resistance between its parallel faces is 4.
As the value of the ratio of maximum to minimum resistance between its parallel faces is 4, thus, option (A) is correct.

Note: The units of the physical parameters should be known. The formula for computing the maximum resistance and the formula for computing the minimum resistance should be known to solve this problem.