Question

The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are $1m$ and $1.2m$ and perpendicular distance between them is $0.8m$.
A. $0.37{m^2}$
B. $0.47{m^2}$
C. $0.88{m^2}$
D. $0.67{m^2}$

Answer 1

Hint: We know that area of a Trapezium is half times the product of its height and sum of parallel sides, or $A = \dfrac{1}{2}h\left( {a + b} \right)$. We will use this formula, and substitute the given values of parallel sides and height to obtain the area of trapezium.

Complete step by step answer:

Diagram:

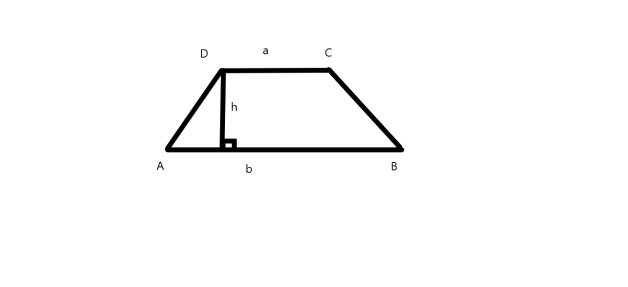
A trapezium is a quadrilateral having a pair of lines parallel to each other. For a trapezium ABCD, having AB and CD as parallel lines, the height of a trapezium is defined as the distance between the parallel lines AB and CD
Now, we know the formula for the area of a trapezium, i.e.
$A = \dfrac{1}{2}h\left( {a + b} \right)$
where A is the area of trapezium,
$h$is the height of trapezium or the distance between the parallel lines,
$a$and $b$are the parallel sides of trapezium,
Now according to given data, parallel sides are $1m$ and $1.2m$ and perpendicular distance between the parallel lines is $0.8m$
$\Rightarrow a = 1m$
$\Rightarrow b = 1.2m$
$\Rightarrow h = 0.8m$
Using the above formula, and substituting the above values
$A = \dfrac{1}{2}h\left( {a + b} \right)$
Area of trapezium is:
$A = \dfrac{1}{2} \times 0.8 \times \left( {1 + 1.2} \right){m^2}$
$\Rightarrow A = \dfrac{1}{2} \times 0.8 \times 2.2{m^2}$
$\Rightarrow A = 0.4 \times 2.2{m^2}$
$\Rightarrow A = 0.88{m^2}$
Thus, Area of trapezium calculated by above formula is $0.88{m^2}$
Hence, option C $0.88{m^2}$ is correct
Note: While calculating the area the formula must be remembered, and there should not be any confusion in determining the parallel sides of the trapezium. The formulas for areas of various plane figures are mentioned below which needs to be remembered by students to solve these types of problems easily and quickly.
Area of square with side a: ${a^2}$
Area of a triangle with base ‘b’ and height ‘h’:$\dfrac{1}{2} \times b \times h$
Area of circle with radius r: $\pi {r^2}$
Area of the rectangle with length l and breadth b: $l \times b$