Question

The reverse breakdown voltage of a Zener diode is 5.6 V in the given circuit. The current ${{I}_{Z}}$ through the Zener is

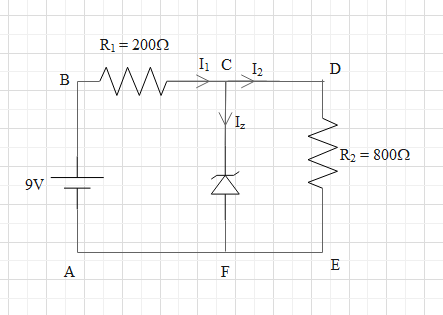
A. 7mA
B. 17mA
C. 10mA
D. 15mA

Answer 1

Hint: Use Ohm’s law which gives us the equation V = IR. Kirchhoff's voltage law finds the current flowing in the two resistances. Once you find the current in the two resistances then use junction law to find ${{I}_{Z}}$.

Formula used:
V = IR

Complete step by step answer:
Reverse breakdown voltage of a diode is the minimum voltage at which the diode starts to conduct electricity in reverse bias. Otherwise, in reverse biased a diode does not conduct electricity. In other words, it acts as an insulator.
Let the potential difference across the Zener diode be ${{V}_{Z}}$.
Let the resistances 200$\Omega $ and 800$\Omega $ be ${{R}_{1}}$ and ${{R}_{2}}$ and let the potential differences across the resistances ${{R}_{1}}$ and ${{R}_{2}}$ be ${{V}_{1}}$ and ${{V}_{2}}$ respectively.
According to ohm’s law, V = IR.
Let the current passing through resistances ${{R}_{1}}$ and ${{R}_{2}}$ be ${{I}_{1}}$ and ${{I}_{2}}$.

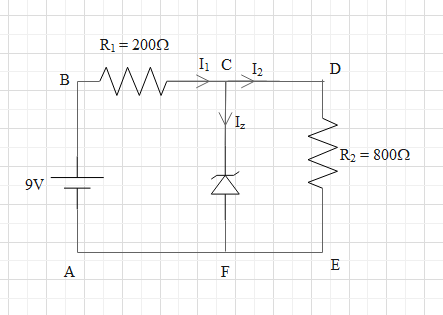
Therefore, ${{V}_{1}}={{I}_{1}}{{R}_{1}}$ and ${{V}_{2}}={{I}_{2}}{{R}_{2}}$.
It is given that the current through the Zener diode is ${{I}_{Z}}$.
Apply Khircoff’s voltage law in loop ABCF in the direction of current (clockwise direction).
Therefore, we get
$9-{{I}_{1}}{{R}_{1}}-{{V}_{z}}=0$.
It is given that ${{V}_{z}}=5.6V$ and ${{R}_{1}}$=200$\Omega $. Substitute the value of ${{V}_{z}}$ and ${{R}_{1}}$ in the above equation.
This implies,
$9-200{{I}_{1}}-5.6=0$.
$\Rightarrow {{I}_{1}}=\dfrac{3.4}{200}=17\times {{10}^{-3}}A=17mA$.
Again, apply Khircoff’s voltage law in loop CDEF in clockwise direction.
Hence we get,
${{V}_{z}}-{{I}_{2}}{{R}_{2}}=0$.
It is given that ${{R}_{2}}$= 800$\Omega $. Substitute the value of ${{R}_{2}}$ and ${{V}_{z}}$ in the above equation.
This gives,
${{I}_{2}}=\dfrac{5.6}{800}=7\times {{10}^{-3}}A=7mA$.
At point C, there is a junction of three currents, ${{I}_{1}}$, ${{I}_{2}}$ and ${{I}_{z}}$.
According to junction law of current, ${{I}_{1}}={{I}_{2}}+{{I}_{z}}$
This gives us that ${{I}_{z}}={{I}_{1}}-{{I}_{2}}$ …… (1).
We found the values of ${{I}_{1}}$ and ${{I}_{2}}$ equal to 17mA and 7mA respectively.
Substitute the values of ${{I}_{1}}$ and ${{I}_{2}}$ in equation (1).
Hence, ${{I}_{z}}=17-7=10mA$.
Therefore, the current flowing through the Zener diode is 10mA.

 Hence, the correct option C.

Note: We can solve the question without knowing Kirchhoff's voltage law.
Assume the potential at the negative terminal of the battery is 0V. Then the potential at the positive terminal is 9V.
The potential difference across the Zener diode is 5.6V. Since the resistance of 800$\Omega $ is in parallel with the Zener diode it will have the same potential difference. Hence, the potential difference across the resistance is 5.6V. This means ${{V}_{2}}$= 5.6V.
Therefore, ${{I}_{2}}=\dfrac{{{V}_{2}}}{{{R}_{2}}}=\dfrac{5.6}{800}=7\times {{10}^{-3}}A=7mA$.
The potential at point F is 0V. The potential difference across the Zener diode is 5.6 V. Current always flows from higher potential to lower potential and when we go from point F to point C, we go in the opposite direction of the current. Hence, the potential will increase by an amount of 5.6V.
Therefore, the potential at point C is 5.6V.
This gives that the potential difference across resistance of 200$\Omega $ is 9 – 5.6 = 3.4V.
Hence, ${{I}_{1}}=\dfrac{{{V}_{1}}}{{{R}_{1}}}=\dfrac{3.4}{200}=17\times {{10}^{-3}}A=17mA$.
At point C, the current ${{I}_{1}}$ divides into two currents ${{I}_{2}}$ and ${{I}_{z}}$. Hence, ${{I}_{1}}={{I}_{2}}+{{I}_{z}}$.