Question

The resultant capacity between the points A and B in the adjoining circuit will be-

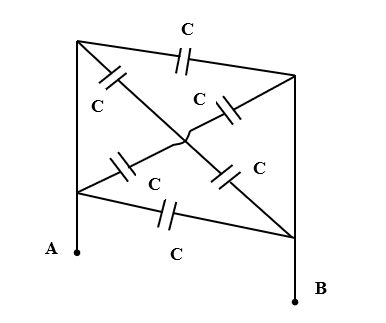
A. C
B. 2C
C. 3C
D. 4C

Answer 1

Hint: To solve this problem, first draw a simplified circuit of the given circuit. It will help you to understand the circuit more easily. Now, the resultant capacity means you have to find the equivalent capacitance from point A to point B. Use the formula for equivalent capacitance which is the addition of all the capacitances. Take care of the capacitances connected in parallel and in series. The obtained equivalent capacitance will be the resultant capacity between the points A and B.

Complete step by step answer:
Simplified version of the given circuit is given below,

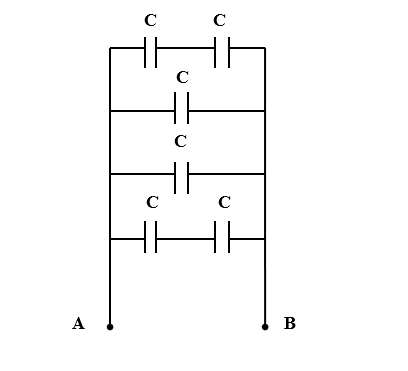
In the circuit drawn above we can divide them into 4 levels.
First level has 2 capacitors. Let them be ${C}_{1}$ and ${C}_{2}$.
Second level has one capacitor. Let it be ${C}_{3}$.
Again, the third level has a single capacitor. Let the capacitor be ${C}_{4}$.
Then the fourth and final level have 2 capacitors. Let it be ${C}_{5}$ and ${C}_{6}$.
Capacitors ${C}_{1}$ and ${C}_{2}$ are connected in series. So, their equivalent capacitance will be,
$\dfrac {1}{{C}_{eq1}}= \dfrac {1}{{C}_{1}}+ \dfrac {1}{{C}_{2}}$
Substituting values in above equation we get,
$\dfrac {1}{{C}_{eq1}}= \dfrac {1}{C}+ \dfrac {1}{C}$
$\Rightarrow \dfrac {1}{{C}_{eq1}}= \dfrac {2C}{{C}^{2}}$
$\Rightarrow {C}_{eq1}= \dfrac {{C}^{2}}{2C}$
$\therefore {C}_{eq1}= \dfrac {C}{2}$
Second level has only a capacitor. So, it’s equivalent capacitance is given by,
$ {C}_{eq2}={C}_{3}$
$\Rightarrow {C}_{eq2}= C$
Similarly, the third level has only a capacitor. So, it’s equivalent capacitance is given by,
$ {C}_{eq3}={C}_{4}$
$\Rightarrow {C}_{eq3}= C$
Capacitors ${C}_{5}$ and ${C}_{6}$ are connected in series. So, their equivalent capacitance will be,
$\dfrac {1}{{C}_{eq4}}= \dfrac {1}{{C}_{5}}+ \dfrac {1}{{C}_{6}}$
Substituting values in above equation we get,
$\dfrac {1}{{C}_{eq4}}= \dfrac {1}{C}+ \dfrac {1}{C}$
$\Rightarrow \dfrac {1}{{C}_{eq4}}= \dfrac {2C}{{C}^{2}}$
$\Rightarrow {C}_{eq4}= \dfrac {{C}^{2}}{2C}$
$\therefore {C}_{eq4}= \dfrac {C}{2}$
All the levels are in parallel. So, the equivalent capacitance is given by,
${C}_{eq} = {C}_{eq1}+ {C}_{eq2}+ {C}_{eq3}+ {C}_{eq4}$
Substituting values in above equation we get,
${C}_{eq}= \dfrac {C}{2} + C+ C + \dfrac {C}{2}$
$\Rightarrow{C}_{eq}= C + C+ C$
$\therefore{C}_{eq}= 3C$
Hence, the resultant capacity between the points A and B in the given circuit will be 3C.
So, the correct answer is option C i.e. 3C.

Note:
Students should remember that resultant capacitance and resultant resistance have different formulas. So, they should not get confused between them. Formula for resultant capacitance is opposite to the formula for resistance. So, the students should remember these formulas. Capacitances diminish when connected in series. While, they are added up when connected in parallel.