Question

The resonance frequency of the LCR series AC circuit is ${{f}_{\circ }}$. Now the capacitance is made 4 times. Then the few resonance frequencies will be
A. $\dfrac{{{f}_{\circ }}}{4}$
B. $2{{f}_{\circ }}$
C. ${{f}_{\circ }}$
D. $\dfrac{{{f}_{\circ }}}{2}$

Answer 1

Hint: LCR circuit is a circuit when a passive components resistor, inductor, and capacitor with the AC as a power supply source. Inductors and capacitors are power spring passive devices. In a capacitor current leads voltage by an angle and in an inductor voltage leads the current by an angle.

Complete answer:
Consider a series RLC circuit as shown in the Diagram,
  

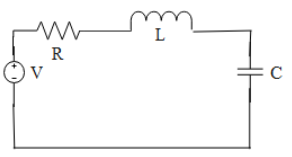
In this circuit, the resistance (R), inductor (L), and capacitor (C) are connected in series along with the provided ac source. The ac current flowing in the circuit changes its direction periodically.
One of the most important properties of the RLC series circuit is the ability to resonate at a particular frequency. And the frequency at the RLC circuit is resonated is known as the resonance frequency. This frequency is measured in hertz. The angular frequency is used which is calculated in radians per second.
Mathematically,
${{\omega }_{\circ }}=2\pi {{f}_{\circ }}$
Where ${{f}_{\circ }}$ is the resonance frequency
This phenomenon occurs because the energy is stored in two forms as electric energy in the capacitor and the magnetic energy in the inductor. The energies are oscillatory in the RLC circuit. At resonance, the impedance of the inductor and the capacitor are equal in magnitude but opposite in direction so that they cancel out each other. Mathematically
$\begin{align}
  & {{X}_{L}}={{X}_{C}} \\
 & \Rightarrow \omega L=\dfrac{1}{\omega C} \\
 & \Rightarrow {{\omega }^{2}}=\dfrac{1}{LC} \\
 & \Rightarrow \omega =\dfrac{1}{\sqrt{LC}} \\
\end{align}$
So at resonance, we can say that the angular frequency can be given as,
${{\omega }_{\circ }}=2\pi {{f}_{\circ }}=\dfrac{1}{\sqrt{LC}}$
Here we can conclude that the resonance frequency of the RLC series circuit is inversely proportional to the square root of the capacitance in the circuit.
${{f}_{\circ }}\propto \dfrac{1}{\sqrt{C}}$
When the value of capacitance is increased by four-time there will be a sudden decrease in the value of the resonance frequency by two times.

Thus the correct option which shows the true value of frequency as asked in the question is Option D.

Note:
The resonance frequency is always calculated in radians for mathematical convenience. It is dependent on the magnitude of the inductance and the capacitance used in the circuit but it is not dependent on the direction. There is no effect of resistance on the resonance frequency of the circuit because the resistor is a passive element that cannot store energy and shows linear properties.