Question

The resistances of the four arms P, Q, R, and S in a Wheatstone’s bridge are $10\Omega $, $30\Omega $, $30\Omega $ and $90\Omega $, respectively. The e.m.f. and the internal resistance of the cell are $7V$ and $5\Omega $ respectively. If the resistance of the galvanometer is $50\Omega $, the current drawn from the cell will be
(a). $1.0A$
(b). $0.2A$
(c). $0.1A$
(d). $2.0A$

Answer 1

- Hint: Draw the circuit diagram for the question, apply the principle of Wheatstone bridge, resolve the circuit and find its equivalent resistance to find the value of current drawn.
Formulae used: Formulae for finding the equivalent resistance in a circuit:
\[\begin{align}
  & \text{For series }\Rightarrow \text{ }{{\text{R}}_{eq}}={{\text{R}}_{1}}+{{\text{R}}_{2}} \\
 & \text{For parallel }\Rightarrow \text{ }{{\text{R}}_{eq}}=\dfrac{{{\text{R}}_{1}}{{\text{R}}_{2}}}{{{\text{R}}_{1}}+{{\text{R}}_{2}}} \\
\end{align}\]
Formula for Ohm’s law:
$V=IR$

Complete step-by-step solution -

Wheatstone bridge is an instrument which is used to measure the unknown resistance connected in a circuit. It consists of four resistors of which two resistors are known resistors, one resistor which can be varied and the unknown resistor. It also consists of a galvanometer. Refer to the connections from the figure.

It works on the principle that when the value of resistors follows the relation
$\dfrac{P}{Q}=\dfrac{R}{S}$
the voltages at point b and d become the same and the current in the galvanometer G becomes zero.
In this question we have
$\begin{align}
  & P=10\Omega \\
 & Q=30\Omega \\
 & R=30\Omega \\
 & S=90\Omega \\
\end{align}$
Therefore,
\[\dfrac{P}{Q}=\dfrac{10}{30}=\dfrac{R}{S}=\dfrac{30}{90}=\dfrac{1}{3}\]
Thus, no current flows in the galvanometer. And the effective circuit looks like this.
We know,
\[\begin{align}
  & \text{For series }\Rightarrow \text{ }{{\text{R}}_{eq}}={{\text{R}}_{1}}+{{\text{R}}_{2}} \\
 & \text{For parallel }\Rightarrow \text{ }{{\text{R}}_{eq}}=\dfrac{{{\text{R}}_{1}}{{\text{R}}_{2}}}{{{\text{R}}_{1}}+{{\text{R}}_{2}}} \\
\end{align}\]
Equivalent resistance of the circuit is calculated as follows:

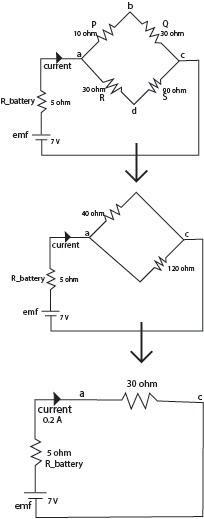
\[\begin{align}
  & {{R}_{eq\_up}}=P+Q=40\Omega \\
 & {{R}_{eq\_down}}=R+S=120\Omega \\
 & {{R}_{eq}}=\dfrac{{{R}_{eq\_up}}{{R}_{eq\_down}}}{{{R}_{eq\_up}}+{{R}_{eq\_down}}}=\dfrac{40\times 120}{40+120}=\dfrac{4800}{160}=30\Omega \\
\end{align}\]
From the relation of voltage, current and resistance in a circuit
$V=IR$
The current can be calculated as
$I=\dfrac{V}{{{R}_{battery}}+{{R}_{eq}}}=\dfrac{7}{30+5}=\dfrac{7}{35}=0.2A$
Therefore, the answer to this question is option B. $0.2 A$.

Note: The value of the resistance in the galvanometer is redundant. Do not use that value and complicate the question. Since, in a Wheatstone’s bridge no current flows through the branch with the galvanometer there is no voltage difference because of the resistance in the galvanometer.