Question

The relation between RMS velocity, average velocity and most probable velocity is:
A: RMS velocity> average velocity > most probable velocity.
B: average velocity> RMS velocity> most probable velocity
C: RMS velocity= average velocity> most probable velocity
D: most probable velocity> average velocity> RMS velocity

Answer 1

Hint:
The kinetic molecular theory states that the gas molecules are continuously moving in random motion. During their motion, different molecules have different velocities and the molecules keep on colliding with each other. Velocity is used to describe the movement of gas molecules.

Complete step by step answer:
We need to derive the relation between the three types of velocities, that are RMS velocity, average velocity and most probable velocity. Before deriving the relation, we must know a little detail about them.
Root mean square velocity:
The relation between temperature and kinetic energy is
${E_k} = \dfrac{3}{2}RT$
And the relation of kinetic energy is
${E_k} = \dfrac{1}{2}m{v^2}$
On combining these two equations we get:
${V^2} = \dfrac{{3RT}}{m}$
Or ${V_{rms}} = \sqrt {\dfrac{{3RT}}{M}} $
Thus we can say that the root means square velocity as square root of average square velocity.
In the equation, R is gas constant, T is temperature and M is molar mass in kg/mol of molecule.
Average velocity:
Average velocity is the rate of change of position of an object. It can also be explained as total displacement in total time.
${V_{avg}} = \dfrac{{8RT}}{{\pi M}}$
Most probable velocity:
The velocity which is possessed by the maximum fraction of gaseous molecules at a particular time is known as most probable velocity.
Its formula is:
${V_{mp}} = \sqrt {\dfrac{{2RT}}{M}} $
If we compare these velocities, their ratio would be:
 ${V_{rms}}:{V_{avg}}:{V_{mp}}$
$\sqrt {\dfrac{{3RT}}{M}} :\sqrt {\dfrac{{8RT}}{{\pi m}}} :\sqrt {\dfrac{{2RT}}{M}} $
R,T and M are present in all the three so they will cancel out.
$\sqrt 3 :\sqrt {\dfrac{8}{\pi }} :\sqrt 2 $
1.732: 1.596: 1.414
Therefore, the ratio of ${V_{rms}},{V_{avg}},{V_{mp}}$ is 1.732: 1.596: 1.414.
It shows that ${V_{rms}}$ is greatest and ${V_{mp}}$ have least value.
So RMS velocity> average velocity > most probable velocity.
Hence, the correct option Is (A).

Note:The distribution of magnitude of velocity of gas is shown with the help of maxwell-boltzmann curve.
            

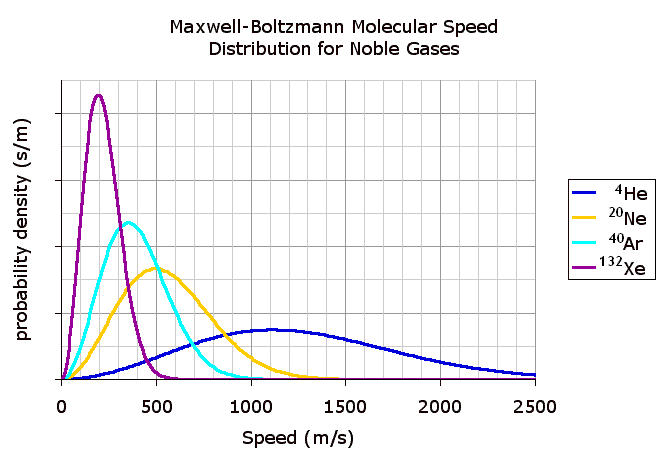
RMS velocity is used in place of average velocity because typical gas molecules move in all directions and have net zero velocity.