Question

The relation between edge length ($a$) and radius of atom ($r$) for FCC lattice is $\sqrt{2}a=4r$.
(A) True
(B) False

Answer 1

Hint: Try to recall that FCC lattice has pointed at all the corners as well as at the centre of each of the six faces of the cube. Consider the full form of FCC which is face-centred cubic. Now, by using this you can easily find if the given statement is true or false.

Complete step by step solution:
-We know that in face centred cubic (FCC) arrangement, there is one atom at each of the eight corners of a cube and that atom present at each corner contributes 1/8 to a cube because it is shared by 8 cubes.
-Also, in a face-centred cube, the atoms along the face diagonal of the cube touch each other.
-In the face-centred cubic arrangement, the three atoms along with the face diagonal touch each other as shown in the below figure:

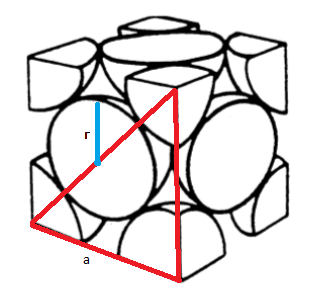
- We can use the Pythagorean theorem to calculate the value of the edge of the cell. We know that the sides are labelled as $a$. The hypotenuse of the triangle will be equal to four times the value of the radius. This will happen since the hypotenuse passes through the diameter of one of the atoms at the centre of the face and two radii of the atoms placed at the edges. So, we can formulate the equation as:
\[\begin{align}
& {{(hypotenuse)}^{2}}={{a}^{2}}+{{a}^{2}} \\
& {{(4r)}^{2}}=2{{a}^{2}} \\
& {{a}^{2}}=8{{r}^{2}} \\
\end{align}\]
Now, solving for $a$ by taking the root:
\[a=2\sqrt{2}r\]
Multiplying by $\sqrt{2}$ on both sides, we get:
\[\sqrt{2}a=4r\]

Therefore, from above we can conclude that the given statement is true and option A is the correct answer to the given statement.

Note: Note that a face centred cubic unit cell has four atoms per unit cell. Also, you should remember that there are six atoms at the faces of each cube and each is shared by two unit cells. Therefore, the contribution of each atom at the face per unit cell is 1/2.