Question

The region between two concentric spheres of radii ‘a’ and ‘b’, respectively, has a volume charge density of $\rho =\dfrac{A}{r}$, where A is constant and r is the distance from the centre. At the centre of the sphere is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:

A. $\dfrac{Q}{2\pi {{a}^{2}}}$
B. $\dfrac{Q}{2\pi ({{b}^{2}}-{{a}^{2}})}$
C. $\dfrac{Q}{2\pi ({{a}^{2}}-{{b}^{2}})}$
D. $\dfrac{Q}{\pi {{a}^{2}}}$

Answer 1

Hint: This question is an application of the concept of Flux that was given by Gauss. We can easily find the formula using Gauss's Theorem. Take a small element dr and then integrate. While integrating, set a and b as lower limit and upper limit respectively.

Complete answer:
Let us consider a sphere between two concentric spheres lying in the area of radius r and thickness dr. Charging within alone leads to electric field / flux according to Gauss' theorem.

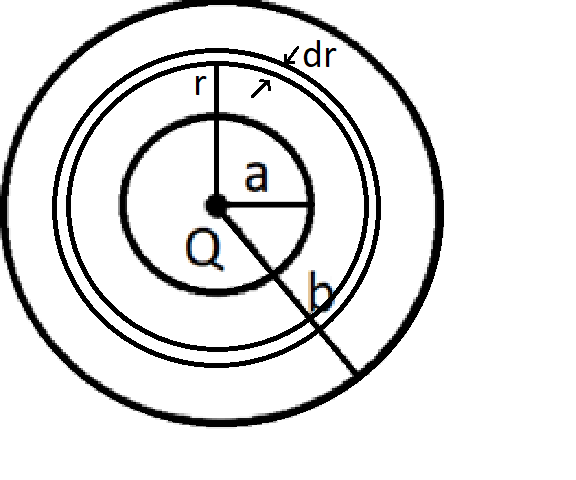
So,
We have
\[\Rightarrow \dfrac{kQ}{{{a}^{2}}}=\dfrac{k[Q+\int\limits_{a}^{b}{4\pi r2drAr}]}{{{b}^{2}}}\]
Where, k is coulomb’s constant, and a, r, and b are the radii of the three concentric circles respectively.
Now,
On integrating, ‘rdr’
In accordance with the power rule of integration, i.e.,
$\int{{{x}^{a}}dx=\dfrac{{{x}^{a+1}}}{a+1}}$
So,
We have
\[\Rightarrow Q\dfrac{{{b}^{2}}}{{{a}^{2}}}=Q+4\pi A[\dfrac{{{r}^{2}}}{2}]_{a}^{b}\]
\[=Q+4\pi A\dfrac{({{b}^{2}}-{{a}^{2}})}{2}\]
\[\Rightarrow \dfrac{Q\left( {{b}^{2}}-{{a}^{2}} \right)}{{{a}^{2}}}=2\pi A\left( {{b}^{2}}-{{a}^{2}} \right)\]
So, now
We have
\[A=\dfrac{Q}{2\pi {{a}^{2}}}\]
So, the value of A such that the electric field in the region between the spheres will be constant, is \[\dfrac{Q}{2\pi {{a}^{2}}}\]

So, the correct answer is “Option A”.

Note:
The law of Gauss, also known as the flux theorem of Gauss, is a law of physics relating to the propagation of electric charges to the resulting electric field. A closed one enclosing a volume such as a spherical surface might be the surface under consideration.