Question

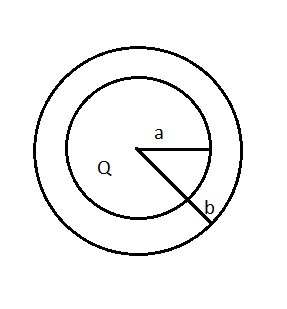
The region between two concentric circle spheres of radius and , respectively (in figure), has volume charge density $ \rho = \dfrac{A}{r} $ , where $ A $ is a constant and $ r $ is the distance from the centre. At the centre of the sphere is a point charge $ Q $ . The value of $ A $ such that the electric field in the region between the spheres will be constant, is:

(A) $ \dfrac{Q}{{2\pi {a^2}}} $
(B) $ \dfrac{Q}{{2\pi \left( {{b^2} - {a^2}} \right)}} $
(C) $ \dfrac{Q}{{2\pi \left( {{a^2} - {b^2}} \right)}} $
(D) $ \dfrac{{2Q}}{{\pi {a^2}}} $

Answer 1

Hint: to solve this problem we should know about the Gauss’s theorem and force exerted by electric charge.
Electrostatic force:
 $ F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}} $ , here $ k $ is constant.
Gauss’s theorem: it states that the net flux through any hypothetical closed surface will equal to $ \dfrac{1}{{{\varepsilon _0}}} $ times the total charge inside the closed surface.
  $ \oint {E.ds = \dfrac{1}{{{\varepsilon _0}}}q} $

Complete step by step solution:
Let’s assume that a sphere of radius $ r $ and it has thickness $ dr $ lying in the region between two concentric spheres.
From Gauss's theorem, charge inside alone will contribute to the electric field. We get,
So, $ \dfrac{{kQ}}{{{a^2}}} = \dfrac{{k\left[ {Q + \int\limits_a^b {4\pi {r^2}dr\dfrac{A}{r}} } \right]}}{{{b^2}}} $
  $ \Rightarrow Q\dfrac{{{b^2}}}{{{a^2}}} = Q + A\int\limits_a^b {4\pi rdr} $
By integrating the given equation. We get,
  $ \Rightarrow Q\left( {\dfrac{{{b^2}}}{{{a^2}}} - 1} \right) = 2\pi A({b^2} - {a^2}) $
  $ \Rightarrow Q\left( {\dfrac{{{b^2} - {a^2}}}{{{a^2}}}} \right) = 2\pi A({b^2} - {a^2}) $
  $ \Rightarrow A = \dfrac{Q}{{2\pi {a^2}}} $
So, we can conclude from the above solution, option (a) is the right answer.

Note:
Gauss’s law is used to solve complex problems. As we have to only find the charge inside the given surface then we can easily calculate the electric field due to these charges. We can find complex problems like electric fields due to infinite long charge carrying wire, electric field due to charge plate, electric field due to charged cylinder. Electric field is a force experienced by a charged particle in the periphery of another charged particle.