Question

The ratio of the areas of the incircle and circumcircle of square is:
A) \[1:\sqrt 2 \]\[\]
B) \[1:\sqrt 3 \]
C) \[1:4\]
D) \[1:2\]

Answer 1

Hint: A Square circumscribing a circle and another square is inscribed in a circle with one vertex at the point of contact indicates that the one square is circumscribed to a circle and another one is inscribed.

Area of square\[ = {a^2}\]\[ = sid{e^2}\]
Diagonal of square \[ = \sqrt {2\,\,} a\]


Complete step-by -step solution:
Given that a square circumscribed a circle and another square is inscribed in the circle with one vertex at the point of contact let the radius of the circle\[ = r\]

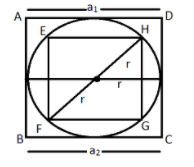
Now in square EFGH, we have:
Diagonal of square \[ = \sqrt {2\,\,} a\]
Diagonal of circle = \[2r\]
In EFGH, \[a = {a_2}\]
As here in the diagram, diagonal of the square is equal to diagonal of the circle. We have:
\[2r = \sqrt 2 \,{a_2}\]
\[{a_2} = \dfrac{{2r}}{{\sqrt 2 }} = \sqrt 2 r........(1)\]
Area of square EAGH is:
  \[
  {A_{EAGH}} = \left( {{a_2}} \right){}^2 \\
   = {(\sqrt 2 r)^2} \\
   = 2{r^2}.......(2) \\
 \]
Now, considering the square ABCD:
Diagonal of square \[ = \sqrt {2\,\,} a\]
Diagonal of circle = \[2r\]
In EFGH, \[a = {a_1}\]
As here in the diagram, diagonal of the square is equal to diagonal of the circle. We have:
\[{a_1} = 2r\]
Area of square ABCD is:
 \[
  {A_{ABCD}} = {({a_1})^2} \\
   = {(2r)^2} \\
   = 4{r^2}.......(3) \\
 \]
Now Ratio of Area of square EFGH and area of square ABCD is:
\[
  \dfrac{{{A_{EFGH}}}}{{{A_{ABCD}}}} = \dfrac{{2{r^2}}}{{4{r^2}}} \\
   = \dfrac{1}{2} \\
 \] (from \[e{q^n}\](2) & (3))
Hence, the areas of the inscribed and circumscribed squares are $1:2$

Hence the correct answer is option D.

Note:In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The centre of this circle is called the circumcenter, and its radius is called the circumradius. A circumscribed square of a circle is a square surrounding a circle such that the circumference of the circle touches the midpoints of the four sides of the square. The diameter of the circle is equal to the side length of the square.