Question

The ratio of rectangular planes and diagonal planes in a cubic unit cell is ________.
A) 1:2
B) 3:1
C) 2:3
D) 3:4

Answer 1

Hint: Imagine a cube structure. Find the number of planes that are parallel to the sides of the cube and these will be the rectangular planes. Also, find the number of planes that can go through the opposite edges of the cube and these will be the diagonal planes.

Complete step by step answer:
Let us draw a cube unit cell. In the cube, draw the planes parallel to the sides of the cube.
The dashed lines in all the drawn diagrams shows the planes passing in the cube.
After drawing the dashed lines, we get three planes passing in the cube which are parallel to the sides of the cube, hence, these are rectangular planes. The three rectangular planes in the cube are shown below with the help of diagram:
     

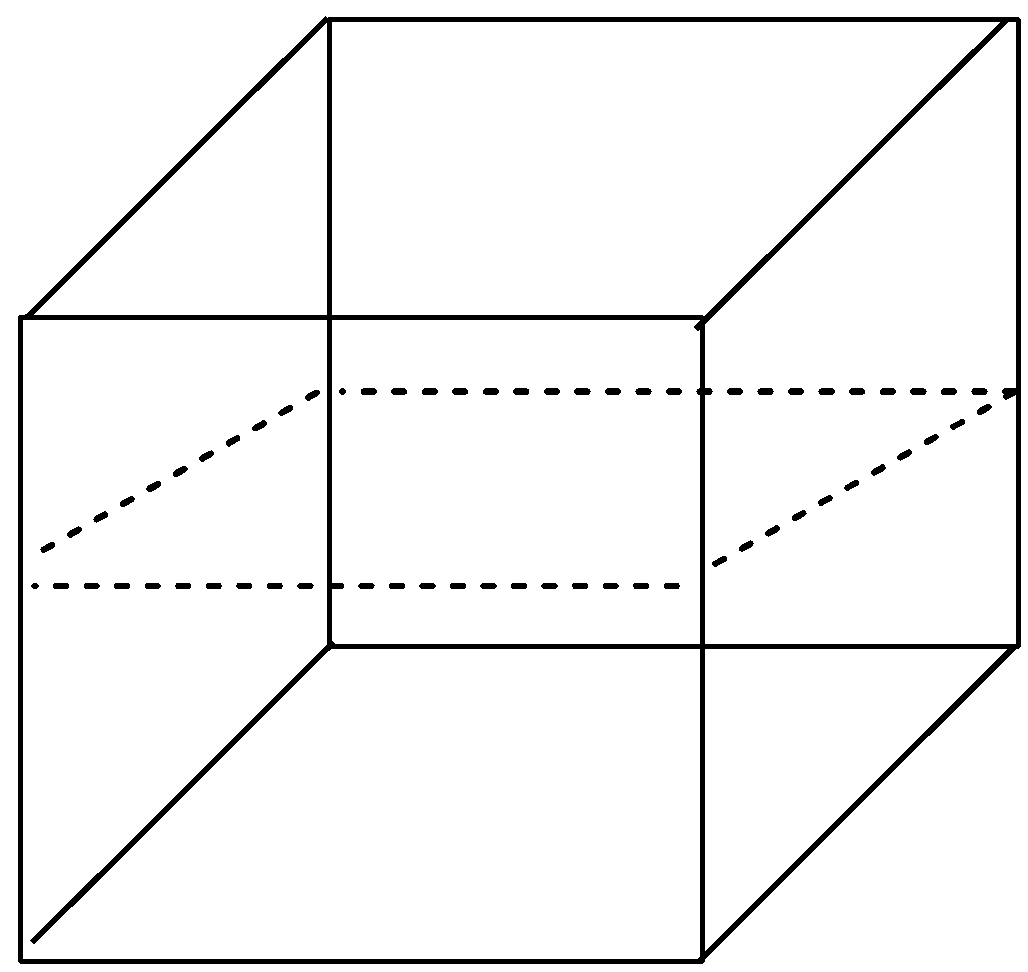
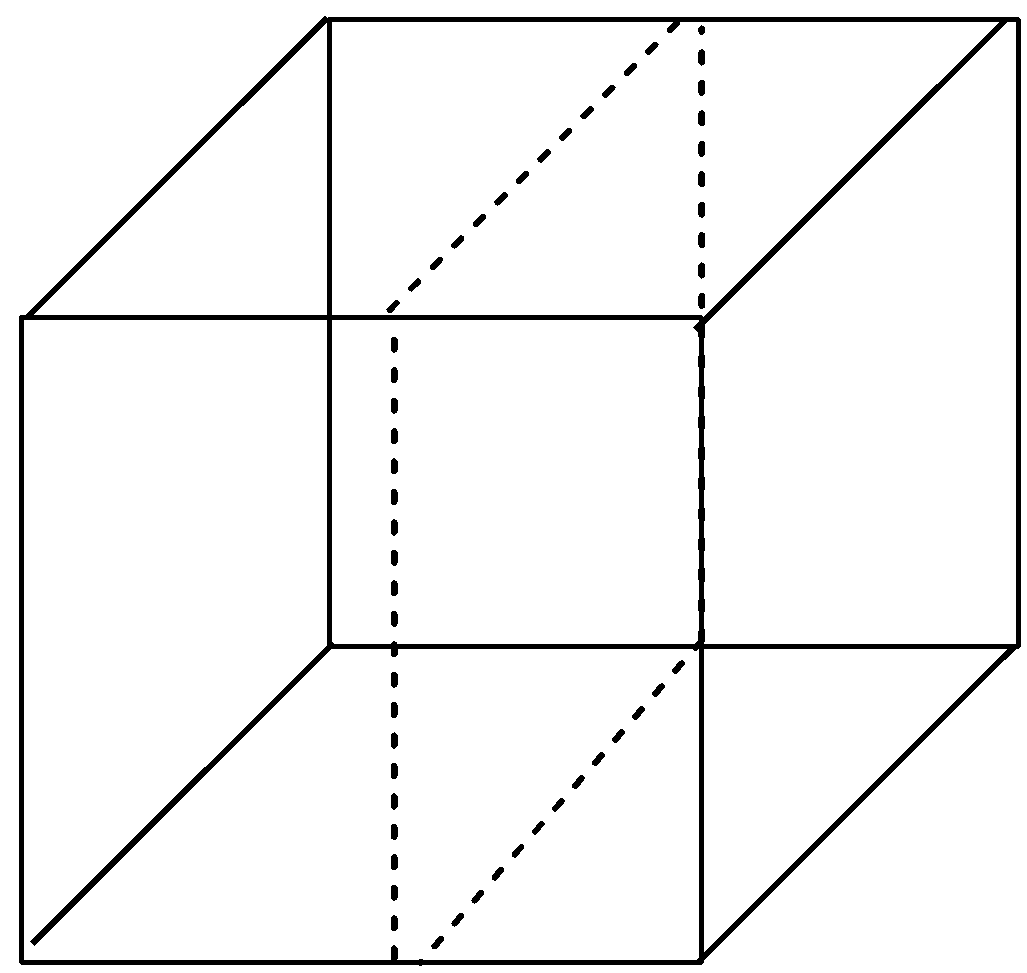
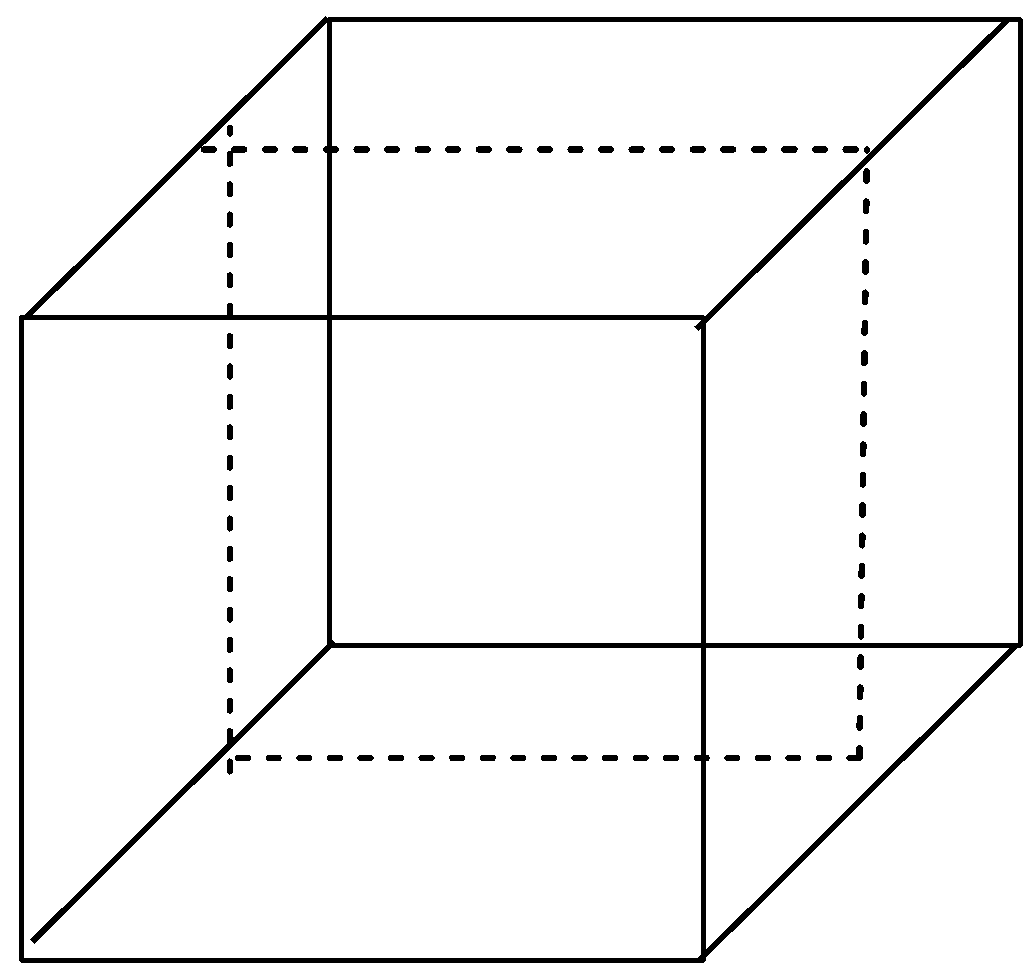
Now, let us imagine a cube again but this time we have to think of the planes that can go through the opposite edges of the cube. There are 6 planes that cut the cute through opposite edges and hence these are diagonal planes as they are passing through the diagonals in the cube. The 6 diagonal planes in the cube are shown below with the help of diagram:
   

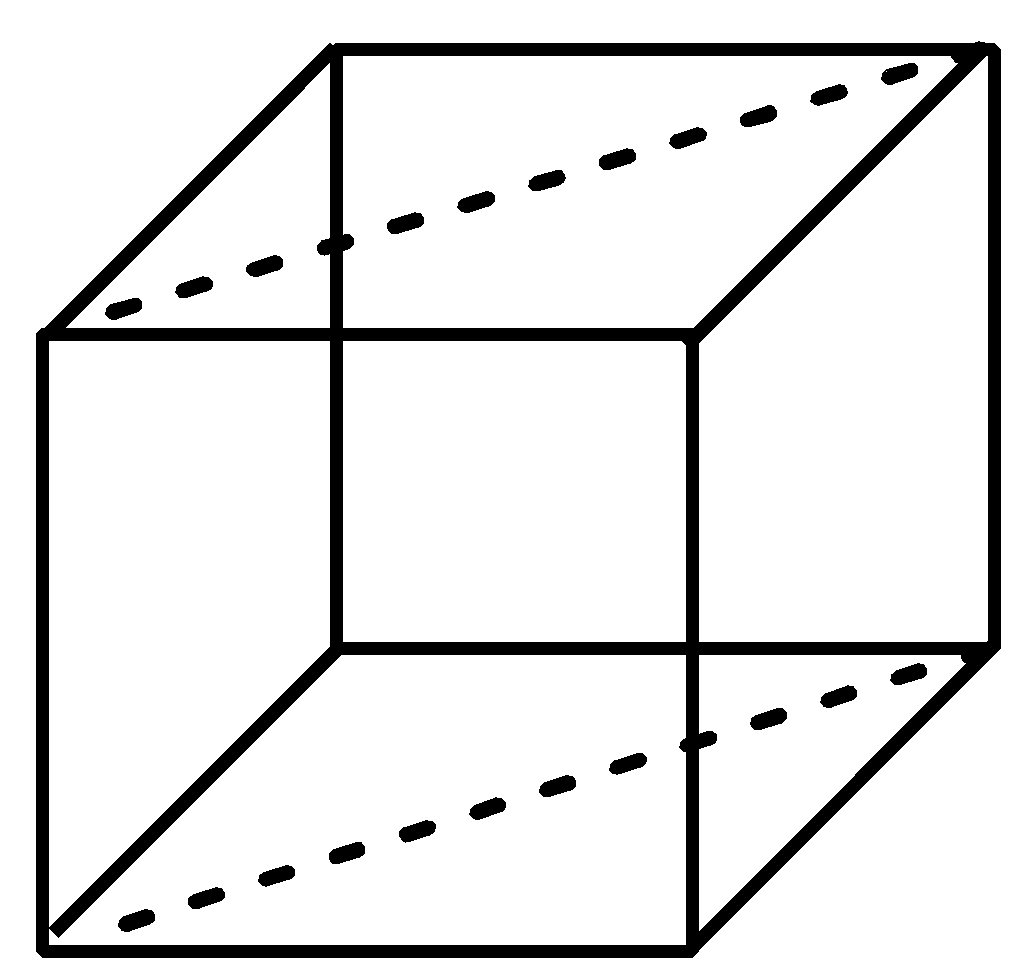
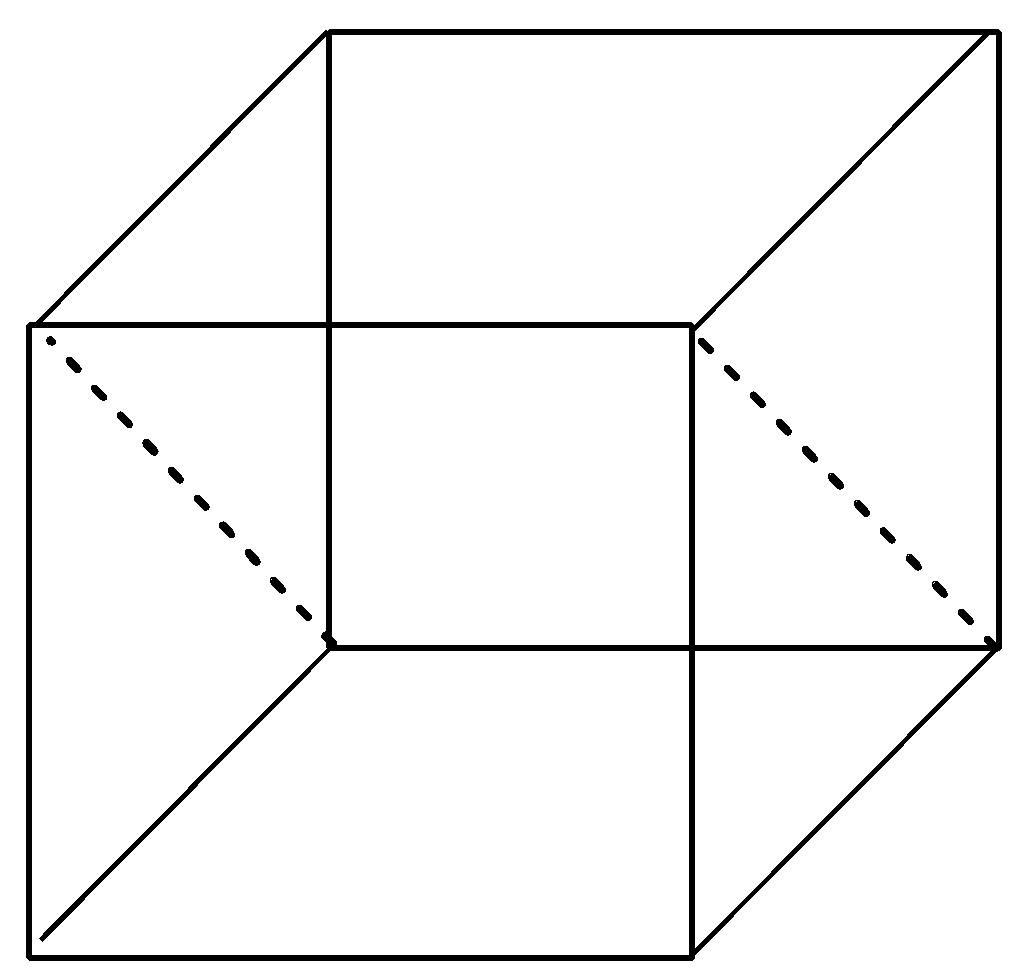
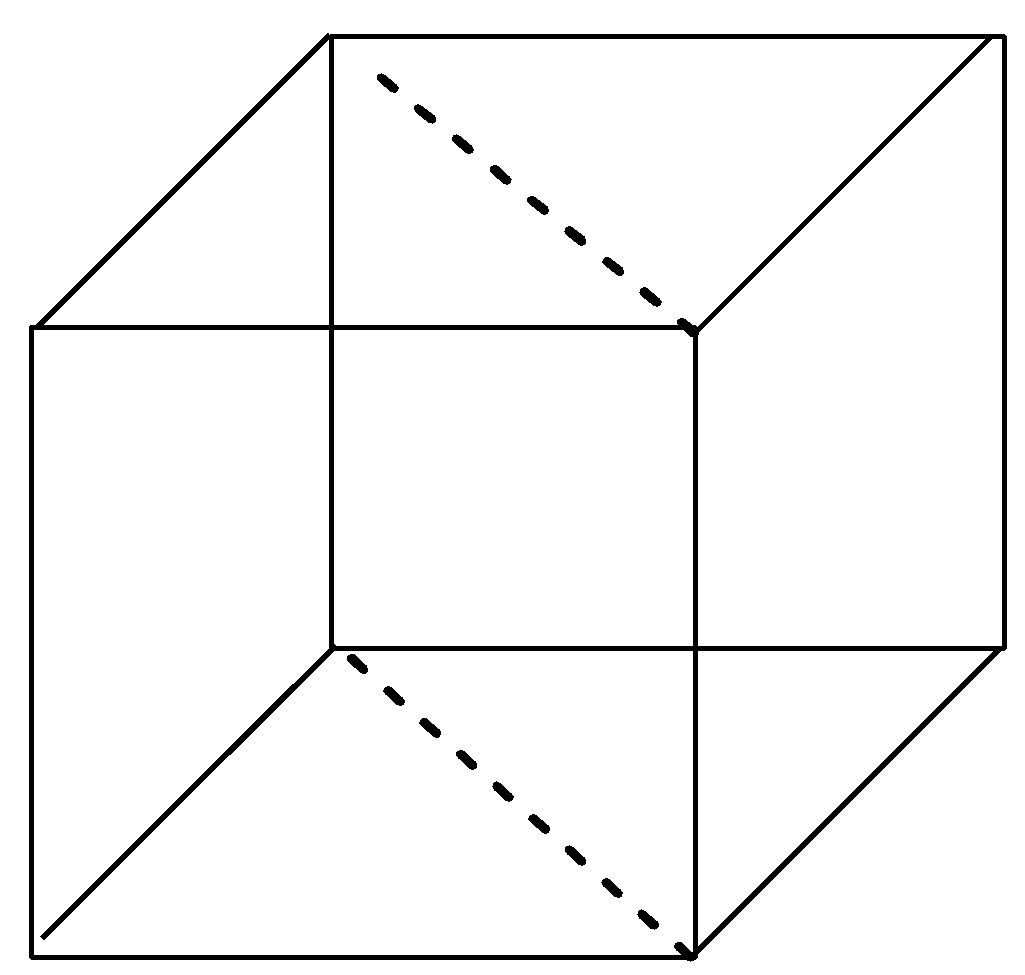
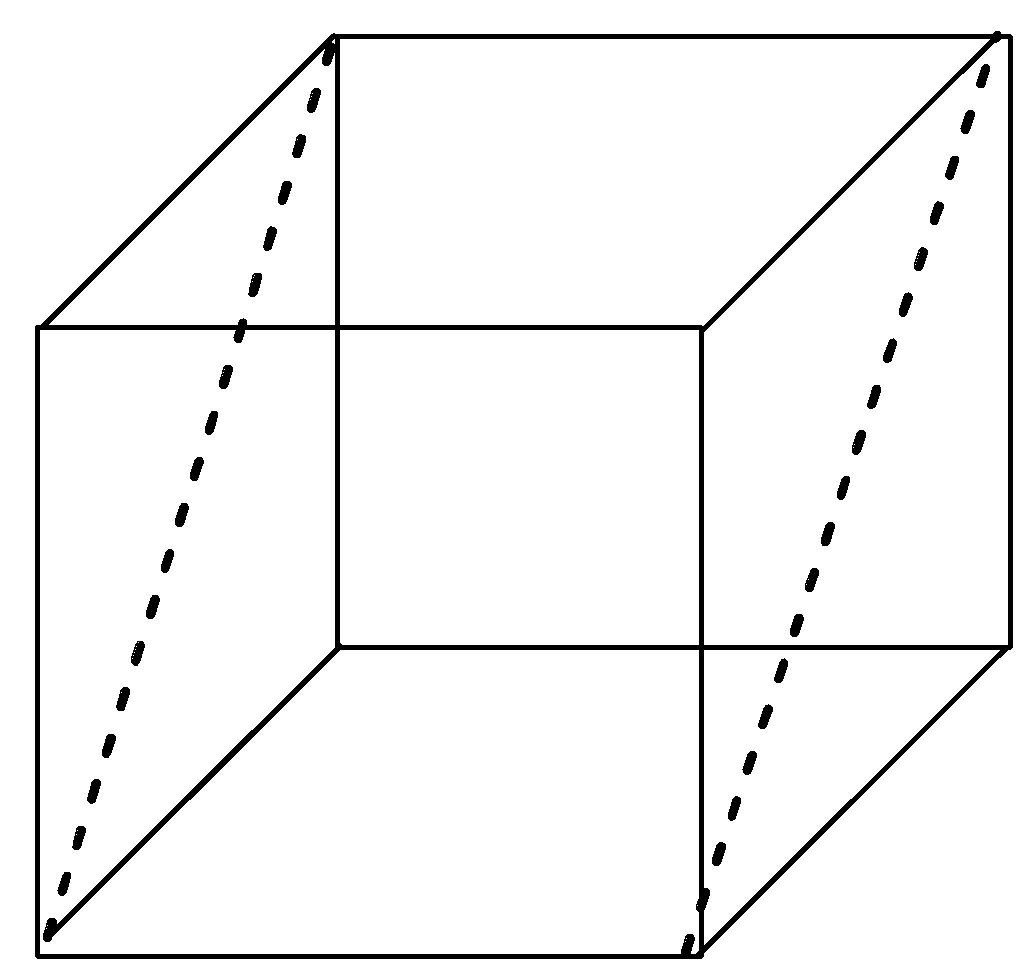
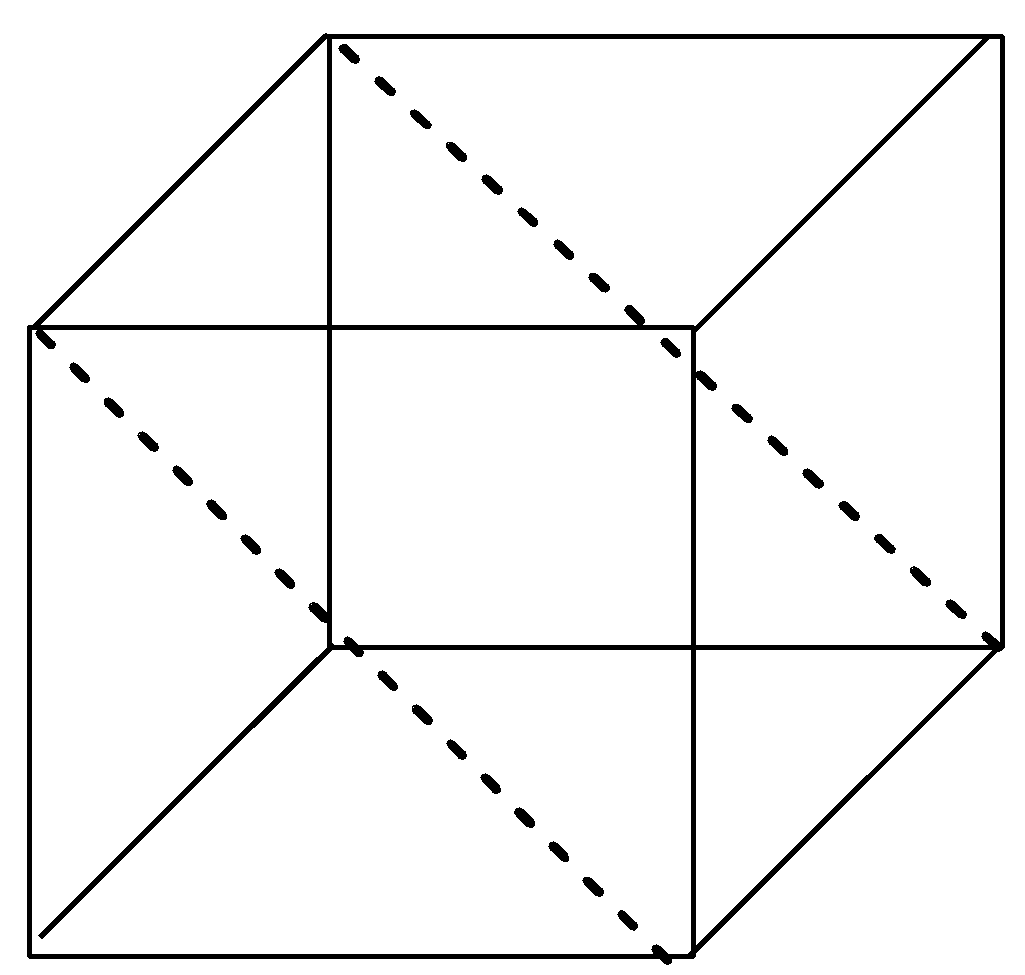
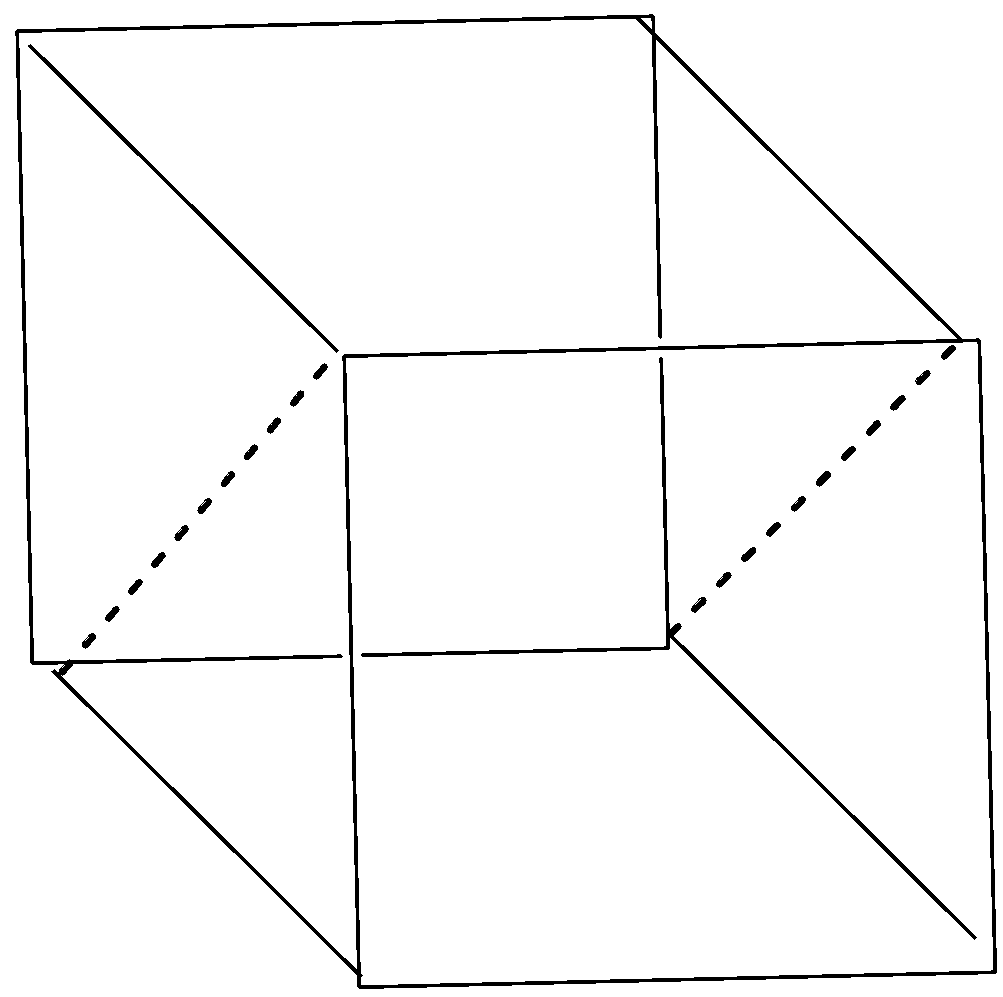
Now, it is quite clear with the above diagrams that rectangular planes are 3 and diagonal planes are 6 in the cube. Hence, the ratio of rectangular planes and diagonal planes in a cubic unit cell is 3:6 or we can write, 1:2.
So, the correct answer is “Option A”.

Note: A unit cell is the smallest portion of a crystal lattice which, when repeated in different directions, makes the entire lattice. In a cubic unit cell, all the edge lengths are equal and all the axial angles are equal to 900.