
The radius of the wheel of bus is \[{\text{35 cm}}\]. How many rotations will a wheel complete while traveling a distance of \[{\text{11Km}}\]
Answer
576.6k+ views
Hint: Distance that will be covered by the wheel in one turn will be equal to its circumference, so it must be rolled several times in order to travel out total \[{\text{11Km}}\]. So we equate them and calculate the number of turns. Also you can use the formula of \[{\text{dist}}{\text{. = (no}}{\text{.ofturns)(circumference)}}\]. As we know the radius of the wheel so calculate it’s circumference using \[{\text{2$\pi$ r}}\].
Complete step by step answer:
First of all, calculating the distance covered by the wheel in one rotation :
As per the given values,
\[{\text{r = 35cm}}\]
Diagram:
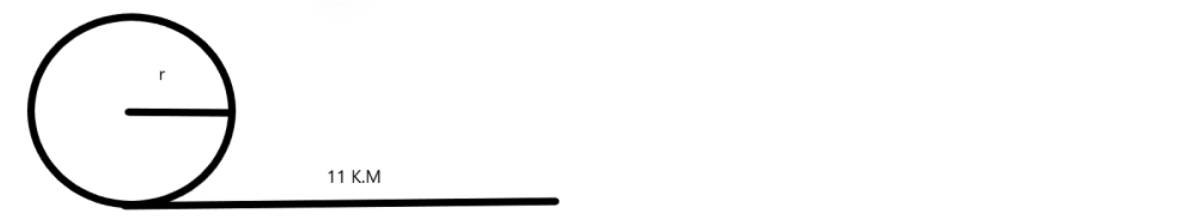
And on substituting it in below formula we get,
\[
\therefore {\text{ Circumference of circle = 2$\pi$ r}} \\
\Rightarrow {\text{2 $\times$ (}}\dfrac{{{\text{22}}}}{{\text{7}}}{\text{) $\times$ 35}} \\
\Rightarrow {\text{2 $\times$ 22 $\times$ 5}} \\
\Rightarrow {\text{220cm}} \\
\Rightarrow {\text{2}}{\text{.2m}} \\
\]
Now , in total wheel has to keep rolling till it will cover \[{\text{11Km = 11}} \times {\text{1000m}}\]
So let the number of turns be n
\[
\Rightarrow {\text{n(2$\pi$ r)}} = 11 \times 1000 \\
{\text{On substituting the value of 2$\pi$ r, we get,}} \\
\Rightarrow {\text{n}}(2.2) = 11000 \\
\Rightarrow {\text{n = }}\dfrac{{{\text{11000}}}}{{{\text{2}}{\text{.2}}}} \\
\therefore {\text{n}} = 5000 \\
\]
Hence to cover \[{\text{11Km}}\] the wheel with \[{\text{35 cm}}\]radius has to rotate almost \[{\text{5000}}\] times.
Note: A circle is a shape consisting of all points in a plane that are a given distance from a given point, the center; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.
The distance around a circle on the other hand is called the circumference (c). A line that is drawn straight through the midpoint of a circle and that has its endpoints on the circle border is called the diameter (d).
Use the value of \[{\text{$\pi$ = }}\dfrac{{22}}{7}\]and solve the equation carefully.
Complete step by step answer:
First of all, calculating the distance covered by the wheel in one rotation :
As per the given values,
\[{\text{r = 35cm}}\]
Diagram:
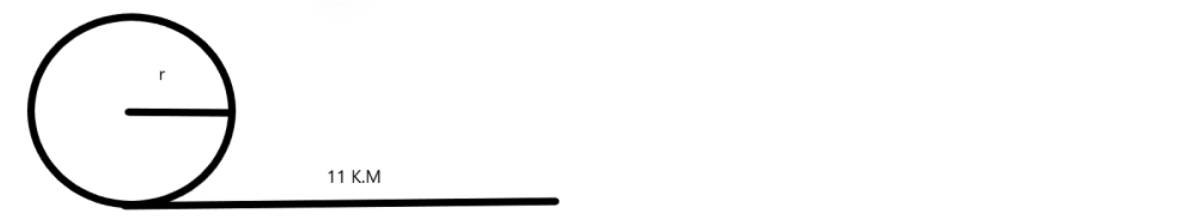
And on substituting it in below formula we get,
\[
\therefore {\text{ Circumference of circle = 2$\pi$ r}} \\
\Rightarrow {\text{2 $\times$ (}}\dfrac{{{\text{22}}}}{{\text{7}}}{\text{) $\times$ 35}} \\
\Rightarrow {\text{2 $\times$ 22 $\times$ 5}} \\
\Rightarrow {\text{220cm}} \\
\Rightarrow {\text{2}}{\text{.2m}} \\
\]
Now , in total wheel has to keep rolling till it will cover \[{\text{11Km = 11}} \times {\text{1000m}}\]
So let the number of turns be n
\[
\Rightarrow {\text{n(2$\pi$ r)}} = 11 \times 1000 \\
{\text{On substituting the value of 2$\pi$ r, we get,}} \\
\Rightarrow {\text{n}}(2.2) = 11000 \\
\Rightarrow {\text{n = }}\dfrac{{{\text{11000}}}}{{{\text{2}}{\text{.2}}}} \\
\therefore {\text{n}} = 5000 \\
\]
Hence to cover \[{\text{11Km}}\] the wheel with \[{\text{35 cm}}\]radius has to rotate almost \[{\text{5000}}\] times.
Note: A circle is a shape consisting of all points in a plane that are a given distance from a given point, the center; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.
The distance around a circle on the other hand is called the circumference (c). A line that is drawn straight through the midpoint of a circle and that has its endpoints on the circle border is called the diameter (d).
Use the value of \[{\text{$\pi$ = }}\dfrac{{22}}{7}\]and solve the equation carefully.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

What are gulf countries and why they are called Gulf class 8 social science CBSE




