Question

The radius of a narrow toroid is ${10^{ - 1}}$$m$ and has $1000$ turns of wire on it. How large current must flow in it, if magnetic induction inside it is $0.05T$.

Answer 1

Hint:Find the magnetic field at a point $P$ due to the current in the solenoid. Then, use this magnetic field to find the current. As it is given that the toroid is narrow, the magnetic field at any point inside the toroid will be the same.

Complete step by step answer:
Toroid is a closed circular solenoid, meaning when a solenoid is bent into a circular shape and the ends of the solenoid are joined, you get a toroid. First consider the cross section of solenoid,

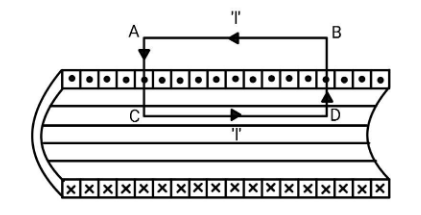
ABCD is a rectangle. There will be two kinds of magnetic field, one parallel to the side AB and the other parallel to the side BD. The magnetic field parallel to the sides AC and BD will cancel due to the adjacent loops on both sides of the rectangle ABCD.

Now, consider a loop which is totally outside the solenoid. The line integral $\int\limits_1^2 {{\mathbf{B}}.{\mathbf{dl}}} = {\mu _0}{I_{enc}}$, since the ${I_{enc}}$ is zero, we have ${B_2} - {B_1} = 0 \to {B_2} = {B_1}$. The magnetic field at infinity will be zero as it is inversely proportional to $r$, the magnetic field outside the solenoid will be zero.
Similarly, the magnetic field outside the toroid will be zero.

Now, to find the magnetic field inside the toroid:
We consider a circle of radius $r$ concentric to the toroid. The line integral $\int {{\mathbf{B}}.{\mathbf{dl}}} $ will be given as,
$\int {{\mathbf{B}}.{\mathbf{dl}}} = \int {Bdl = B\int {dl = 2\pi rB} } $.
According to Ampere’s Law, this integral will be equal to ${\mu _0}{I_{enc}}$ which will be ${\mu _0}NI$. $I$ is the current in the toroid.
Therefore, we have $B = \dfrac{{{\mu _0}NI}}{{2\pi r}}$
$ I = \dfrac{{2\pi rB}}{{{\mu _0}N}}$
Substituting the data provided in the above obtained value,
$I = \dfrac{{\left( {2\pi } \right)\left( {{{10}^{ - 1}}} \right)\left( {0.05} \right)}}{{\left( {4\pi \times {{10}^{ - 7}}} \right)\left( {1000} \right)}}$
$\therefore I = 25A$.

Therefore, a current of $25$amperes should flow in the toroid if magnetic induction inside it $0.05T$.

Note:The toroid is considered to be narrow, that is why we have taken the magnetic field at a distance $r$ inside the toroid to be the same. If the toroid is not narrow, the magnetic field at different radial distances will be different. Due to symmetry, the magnetic on each point of the circle will be the same, that is the reason we took $B$ outside the integral.