Question

The projection of the point $P\left( {\vec{p}} \right)$ on the plane $\vec{r}.\vec{n}=q$ is $\left( {\vec{s}} \right)$, then:
A). $\vec{s}=\dfrac{\left( q-\vec{p}.\vec{n} \right)\vec{n}}{|\vec{n}{{|}^{2}}}$
B). $\vec{s}=\vec{p}+\dfrac{\left( q-\vec{p}.\vec{n} \right)\vec{n}}{|\vec{n}{{|}^{2}}}$
C). $\vec{s}=\vec{p}-\dfrac{\left( \vec{p}.\vec{n} \right)\vec{n}}{|\vec{n}{{|}^{2}}}$
D). $\vec{s}=\vec{p}-\dfrac{\left( q-\vec{p}.\vec{n} \right)\vec{n}}{|\vec{n}{{|}^{2}}}$

Answer 1

Hint: In this question we have to solve this problem by putting the $\vec{r}=\vec{p}+\lambda \vec{n}$ in the $\vec{r}.\vec{n}=q$ then we will calculate the value of $\lambda $ then we will substitute the value of $\lambda $ in $\vec{r}=\vec{p}+\lambda \vec{n}$ and then calculate the value of $\vec{r}$ but $\vec{r}$ is equal to the $\vec{s}$ by this we will calculate the value of the $\vec{s}$ and get the correct option.

Complete step-by-step solution:
So, now in the above question we can get an idea about the projection of point $P\left( {\vec{p}} \right)$ on the plane $\vec{r}.\vec{n}=q$
So, now firstly we draw a plane and its projection points be $\vec{s}$ if we want $\vec{s}$ projection then the direct become $\vec{r}.\vec{n}=q$ here, $\vec{n}$ be the normal and it is parallel

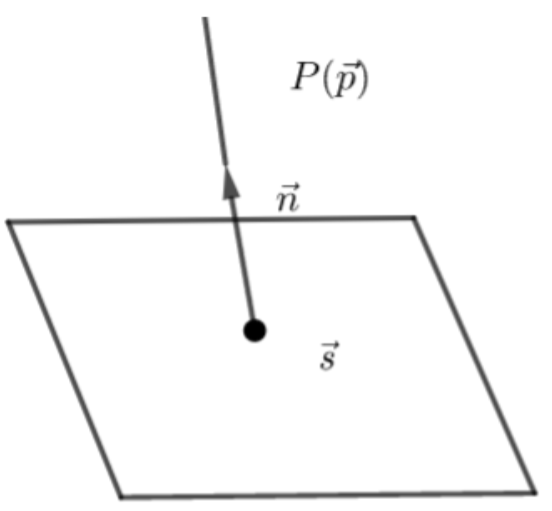
$\vec{r}=\vec{p}+\lambda \vec{n}$……….(as it is parallel to $\lambda $)
This is the equation of line and if the line is intersecting then the value of $\vec{r}$ must satisfy in $\vec{r}.\vec{n}=q$ and that at point we say $\vec{r}=\vec{s}$
After this we will find the dot product
$\left( \vec{p}+\lambda \vec{n} \right).\vec{n}=q$
Then we will multiply $\vec{n}$ to the $\left( \vec{p}+\lambda \vec{n} \right)$ where q is the scalar quantity,
$\vec{p}.\vec{n}+\lambda \vec{n}.\vec{n}=q$
Here $\vec{n}$ and $\vec{n}$ becomes $|\vec{n}{{|}^{2}}$ then we will get,
$\lambda |\vec{n}{{|}^{2}}=q-\vec{p}.\vec{n}$ (scalar);
Here in the below step we will transfer $|\vec{n}{{|}^{2}}$ to the RHS to get the value of $\lambda $.
$\therefore \lambda =\dfrac{q-\vec{p}.\vec{n}}{|\vec{n}{{|}^{2}}}$
Here is the value of $\lambda $
Now, we will put the value of $\lambda $ in $\vec{r}=\vec{p}+\lambda \vec{n}$
After putting the value its simplified value is,
$\vec{r}=\vec{p}+\left( \dfrac{q-\vec{p}.\vec{n}}{|\vec{n}{{|}^{2}}} \right)\vec{n}$
Now, we will substitute $\vec{r}=\vec{s}$ the we will get,
$\vec{s}=\vec{p}+\left( \dfrac{q-\vec{p}.\vec{n}}{|\vec{n}{{|}^{2}}} \right)\vec{n}$
So finally, we get the $\vec{s}$ and the above equation matches with the option B.
Hence the option B. is the correct option.

Note: Here the most important thing is in the vectors to know the difference between Dot product and cross product most of the students are get confuse during exams so here the dot product of u and v is written u ∙ v and is defined two ways:
$u.v={{u}_{1}}{{v}_{1}}+{{u}_{2}}{{v}_{2}}+{{u}_{3}}{{v}_{3}}$
$u.v=|u||v|\cos \theta $ where $\theta $ is the angle formed by u and v.
The two definitions are the same. They are related to one another by the Law of Cosines. The first method of calculation is easier because it is the sum of the products of corresponding components. The second method of calculation can be used if we know the angle $\theta $ formed by u and v.
And The cross product of u and v is defined and best memorized as the expansion of a 3 by 3 determinant:
$u\times v=\left( \begin{matrix}
   i & j & k \\
   {{u}_{1}} & {{u}_{2}} & {{u}_{3}} \\
   {{v}_{1}} & {{v}_{2}} & {{v}_{3}} \\
\end{matrix} \right)=\left( \begin{matrix}
   {{u}_{2}} & {{u}_{3}} \\
   {{v}_{2}} & {{v}_{3}} \\
\end{matrix} \right)i-\left( \begin{matrix}
   {{u}_{1}} & {{u}_{3}} \\
   {{v}_{1}} & {{v}_{3}} \\
\end{matrix} \right)j+\left( \begin{matrix}
   {{u}_{1}} & {{u}_{2}} \\
   {{v}_{1}} & {{v}_{2}} \\
\end{matrix} \right)k$
The cross product of u and v is a vector, with the property that it is orthogonal to the two vectors u and v. Thus, if we take the dot product of u × v with u and then u × v with v, we get zero both times:
 $\left( u\times v \right).u=0,and\left( u\times v \right).v=0$
This check should always be performed to ensure that the cross product is correct.