Question

The power of a lens used to remove the myopic defect of an eye is 0.66D. The far point of this eye is (nearly):
A. 25cm
B. 150cm
C.100cm
D.75cm

Answer 1

Hint: We know that the power is the reciprocal of focal length in meters. We also know that corrective lens is used for a myopic person so as to focus the image of the object at infinity at its far point such that the image formed by eye-lens is now at retina just like any normal eye without defect. So, when we use a corrective lens for a myopic person, the image formed for an object at infinity is at the person’s far point. Recall that, the image formed by any lens of an object at infinity is at its focal point. So, we could get the far point from the focal length of the corrective lens.

Formula used:
The lens formula,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
Expression for power,
$P=\dfrac{1}{f}$

Complete answer:
Let us first understand about the far point for a normal eye.

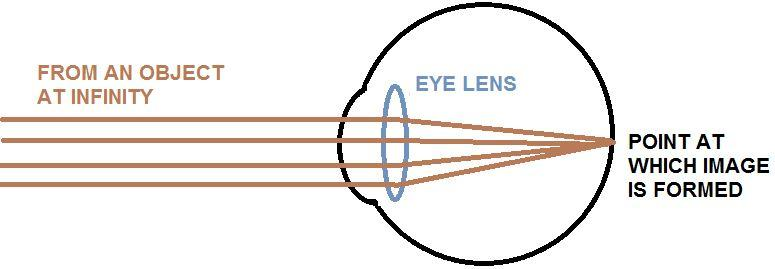
Far point simply is the furthest distance at which our eyes can focus on an object. For a normal eye without any defects, the image of an object at infinity is formed at the retina when the eye is relaxed. That is, the far point for this eye is at infinity.
Myopia or the nearsightedness is that defect in which we can only see the nearby objects clearly but the faraway objects appear blurry. Let us see why this happens.

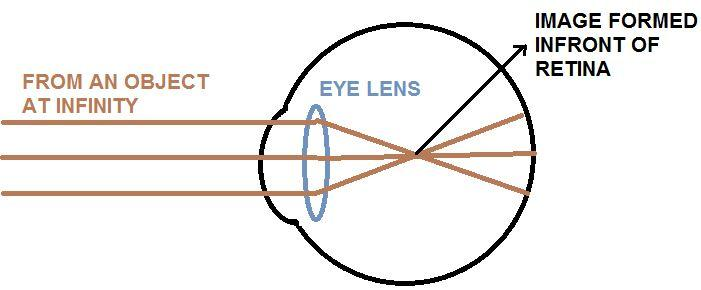
We see that, for a myopic eye, the image of an object at infinity is formed in front of the retina. Unlike normal eyes, the far point of myopic eye is not at infinity but at some point closer than infinity. A myopic eye cannot form an image for an object that lies beyond this far point.
We could use a diverging lens, that is, a biconcave lens to correct this defect.

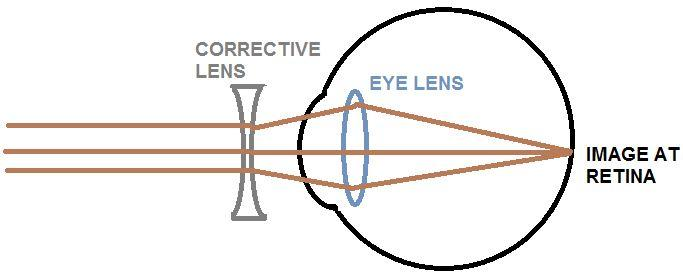
Here, by using a corrective lens we have focused the image of an object at infinity at the person’s far point, so that the person can now focus the image of the same on the retina.
Now that the concept is made clear for you, let us move on to solving the problem.
We know the lens formula which is,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$ ……………….. (1)
Here, f =focal length of the corrective lens
v =far point of the myopic eye (that is where we are supposed to form the image of object at infinity)
u= ∞ (object here is at infinity)
 Now (1) becomes,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{\infty }$
Clearly, $f=v$
In this question we are given the power of the corrective lens as 0.66D, and we also know the relationship between focal length and power of a lens. Power is the reciprocal of focal length (in m).
$f=\dfrac{1}{P}$ ……………… (2)
$\Rightarrow f=\dfrac{1}{0.66D}$
$\Rightarrow f=1.515m$
$\Rightarrow f=151.5cm\approx 150cm$

The answer to the question is option B. f=150cm.

Note:
For equation (2), you should make sure that the focal length is substituted in its SI unit (in meters), because optics related questions are usually dealt in centimeters. Also, conceptual clarity is important to solve any numerical problem so as to avoid time conception in MCQs. For example, here if we know that an image of an object at infinity is formed at a focal point for a lens and this is the far point of a myopic person, we could directly get the answer in one step.