Question

The potential difference between points A and B in the circuit shown in the figure:

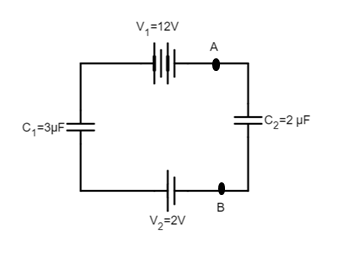
Answer 1

Hint: Use the equation of KVL. The voltages across the capacitors are to write in terms of the charge and corresponding capacitances of the capacitor. In this equation, the charge has to be calculated throughout the circuit. Next, the potential difference between the required points can be found using the calculated values.

Formula used:
Using the KVL we get, $\left( {{V_1} - {V_2}} \right) + {V_{{c_1}}} + {V_{{c_2}}} = 0$
${V_{{c_1}}} = \dfrac{q}{{{C_1}}}$ and ${V_{{c_2}}} = \dfrac{q}{{{C_2}}}$[$q$ is the charge of the circuit.]

Complete step-by-step solution:
Kirchoff’s second law or voltage law states that the algebraic addition of the potential differences around the loop must be equal to zero as: \[\Sigma V = 0\]
The given circuit is:

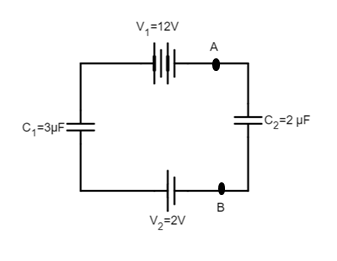
Applying KVL in the above circuit we get,
$\left( {{V_1} - {V_2}} \right) + {V_{{c_1}}} + {V_{{c_2}}} = 0..........(1)$
${V_{{c_1}}} = \dfrac{q}{{{C_1}}}$ and ${V_{{c_2}}} = \dfrac{q}{{{C_2}}}$[$q$ is the charge of the circuit.]
Given that, ${V_1} = 12V$ , ${V_2} = 2V$
${C_1} = 3\mu F = 3 \times {10^{ - 6}}F$, ${C_2} = 2\mu F = 2 \times {10^{ - 6}}F$
Now put the values in eq (1) we get,
$\left( {12 - 2} \right) + \dfrac{q}{{3 \times {{10}^{ - 6}}}} + \dfrac{q}{{2 \times {{10}^{ - 6}}}} = 0$
$ \Rightarrow \dfrac{{5q}}{{6 \times {{10}^{ - 6}}}} = - 10$
$ \Rightarrow q = - \dfrac{{6 \times {{10}^{ - 5}}}}{5}$
\[ \Rightarrow q = - \dfrac{{6 \times {{10}^{ - 5}} \times 2}}{{5 \times 2}}\]
\[ \Rightarrow q = 12\mu C\]
We need to calculate the potential difference of two points A and B i.e ${V_{{c_2}}} = \dfrac{q}{{{C_2}}}$
$\therefore {V_{{c_2}}} = \dfrac{{12 \times {{10}^{ - 6}}}}{{2 \times {{10}^{ - 6}}}} = 6V$
So the answer is $6Volt$.

Note:This law by Kirchhoff is generally known as the Conservation of Energy, since moving around a closed-loop, or circuit, one will end up back to the place where the person started in the circuit and hence back to the similar initial potential with zero loss of voltage throughout the loop. Therefore, the number of voltage drops around the loop should always be equal to the voltage sources met along the way. So during applying Kirchhoff’s voltage law to a certain circuit or loop, it is important to pay special attention to the algebraic signs, (+ and -) of the voltage drops across elements and the emf’s of sources. otherwise, the calculations may be gone wrong.