Question

The points A(4,5,10), B(2,3,4) and C(1,2,-1) are the vertices of a parallelogram ABCD. Find the vector equations of the sides AB and BC and also find the coordinates of point D.

Answer 1

Hint: We will first find the position vectors of points A, B and C. For example, position vector of point A is $\overrightarrow{OA}=4\hat{i}+5\hat{j}+10\hat{k}$. Now, obtain $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$. Then we will use vector equation of line, $\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}$, where $\overrightarrow{a}$ is a point lying on the line and $\overrightarrow{b}$ is a vector parallel to line. In the case of line $\overrightarrow{AB}$, we have $\overrightarrow{a}=\overrightarrow{OA},\overrightarrow{b}=\overrightarrow{AB}$. We will thus get the vector equation of line AB. Similarly for line BC, we will get a vector equation by using, $\overrightarrow{a}=\overrightarrow{OB},\overrightarrow{b}=\overrightarrow{BC}$. In the final step, we will use the concept that diagonals of a parallelogram intersect at the mid-point to find the coordinates of point D.

Complete step-by-step answer:
It is given in the question that the points A(4,5,10), B(2,3,4) and C(1,2,-1) are the vertices of a parallelogram ABCD. And we have been asked to find the vector equations of the sides AB and BC and also find the coordinates of point D.
Let us assume that the coordinates of point D as $\left( \alpha ,\beta ,\gamma \right)$. Then, we can represent A, B, C, D of parallelogram as,

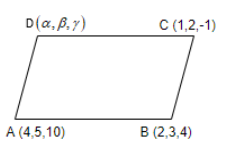
First, we can write the position vectors of all the points as shown below.
$\begin{align}
  & \overrightarrow{OA}=4\hat{i}+5\hat{j}+10\hat{k} \\
 & \overrightarrow{OB}=2\hat{i}+3\hat{j}+4\hat{k} \\
 & \overrightarrow{OC}=\hat{i}+2\hat{j}-\hat{k} \\
 & \overrightarrow{OD}=\alpha \hat{i}+\beta \hat{j}+\gamma \hat{k} \\
\end{align}$
We know that vector $\overrightarrow{AB}$ can be found by subtracting respective position vectors, that is, $\overrightarrow{OB}-\overrightarrow{OA}$, so we get,
$\begin{align}
  & \overrightarrow{AB}=\left( 2-4 \right)\hat{i}+\left( 3-5 \right)\hat{j}+\left( 4-10 \right)\hat{k} \\
 & =-2\hat{i}-2\hat{j}-6\hat{k} \\
\end{align}$
We know that the general vector equation of a line passing through a point with position vector $\overrightarrow{a}$ and parallel to a vector $\overrightarrow{b}$ is given by $\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}$. So, here we have point A, i.e. $\overrightarrow{OA}$ and parallel vector as $\overrightarrow{AB}$, so we can get the vector equation of line AB as,
Vector equation of line AB, $\overrightarrow{r}=\overrightarrow{OA}+\lambda \overrightarrow{AB}$
$\overrightarrow{r}=\left( 4\hat{i}+5\hat{j}+10\hat{k} \right)-\lambda \left( 2\hat{i}+2\hat{j}+6\hat{k} \right)$
We know that vector $\overrightarrow{BC}$ can be found by subtracting respective position vectors, that is, $\overrightarrow{OB}-\overrightarrow{OA}$, so we get,
$\begin{align}
  & \overrightarrow{BC}=\left( 1-2 \right)\hat{i}+\left( 2-3 \right)\hat{j}+\left( -1-4 \right)\hat{k} \\
 & =-\hat{i}-\hat{j}-5\hat{k} \\
\end{align}$
We know that the general vector equation of a line passing through a point with position vector $\overrightarrow{a}$ and parallel to a vector $\overrightarrow{b}$ is given by $\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}$. So, here we have point $\overrightarrow{OB}$ and parallel vector as $\overrightarrow{BC}$, so we can get the vector equation of line BC as,
Vector equation of line BC, $\overrightarrow{r}=\overrightarrow{B}+\mu \overrightarrow{BC}$
$\overrightarrow{r}=\left( 2\hat{i}+3\hat{j}+4\hat{k} \right)-\mu \left( \hat{i}+\hat{j}+5\hat{k} \right)$
We will neglect the negative sign because we are considering only the magnitude here.
Now, we had already assumed the coordinates of point D as $\left( \alpha ,\beta ,\gamma \right)$. As we know that ABCD is a parallelogram and diagonals of a parallelogram intersect at their mid-points, so we get,
Mid-point of diagonal AC = (mid-point of diagonal BD)
We know that coordinates of point A and point C are A(4,5,10) and C(1,2,-1). And the coordinates of point B and point D are, B(2,3,4) and D$\left( \alpha ,\beta ,\gamma \right)$.
Now, we know that from the distance formula, mid-point between any two points can be calculated as,
$x=\dfrac{{{x}_{2}}+{{x}_{1}}}{2},y=\dfrac{{{y}_{2}}+{{y}_{1}}}{2}$
So, we write the mid-point of AC = mid-point of BD as follows,
$\begin{align}
  & \left[ \dfrac{4+1}{2},\dfrac{5+2}{2},\dfrac{10-1}{2} \right]=\left[ \dfrac{\alpha +2}{2},\dfrac{\beta +3}{2},\dfrac{\gamma +4}{2} \right] \\
 & \left[ \dfrac{5}{2},\dfrac{7}{2},\dfrac{9}{2} \right]=\left[ \dfrac{\alpha +2}{2},\dfrac{\beta +3}{2},\dfrac{\gamma +4}{2} \right] \\
\end{align}$
Now, on comparing both the sides, we get,
$\dfrac{\alpha +2}{2}=\dfrac{5}{2}$
On multiplying both the sides with 2, we get,
$\begin{align}
  & \alpha +2=5 \\
 & \alpha =5-2 \\
 & \alpha =3 \\
\end{align}$
Similarly, we get,
$\dfrac{\beta +3}{2}=\dfrac{7}{2}$
On multiplying both the sides with 2, we get,
$\begin{align}
  & \beta +3=7 \\
 & \beta =7-3 \\
 & \beta =4 \\
\end{align}$
And we will get,
$\dfrac{\gamma +4}{2}=\dfrac{9}{2}$
On multiplying both the sides with 2, we get,
$\begin{align}
  & \gamma +4=9 \\
 & \gamma =9-4 \\
 & \gamma =5 \\
\end{align}$
Thus, we get, $\alpha =3,\beta =4,\gamma =5$. So, point D will be $\left( \alpha ,\beta ,\gamma \right)=\left( 3,4,5 \right)$.
So, we can say that the coordinates of point D of the parallelogram is $\left( 3,4,5 \right)$.

Note: We can also use direction ratios and then find vectors $\overrightarrow{AB}\text{ and }\overrightarrow{BC}$. So we have direction ratios of A as (4,5,10) and for B as (2,3,4), now direction ratio of vector AB can be obtained by subtracting the respective direction ratios as (2-4, 3-5, 4-10)=(-2,-2,-6). Then we can write it in vector form as $-2\hat{i}-2\hat{j}-6\hat{k}$ . Also, we can write any vector equation, \[\overrightarrow{r}=\left( a\hat{i}+b\hat{j}+c\hat{k} \right)+\lambda \left( p\hat{i}+q\hat{j}+r\hat{k} \right)\] in Cartesian form as, $\dfrac{\left( x-a \right)}{p}=\dfrac{\left( y-b \right)}{q}=\dfrac{\left( z-c \right)}{r}=\lambda $.