Question

The point which does not lie in the half plane $2x + 3y - 12 \leqslant 0$
(a) (1, 2)
(b) (2, 1)
(c) (2, 3)
(d) (-3, 2)

Answer 1

Hint: Before attempting this question, one should have prior knowledge about line and also remember that the given equation represents a line that exists in a plane, using this information can help you to approach the solution of the question.

Complete step by step answer:
According to the given information we have equation $2x + 3y - 12 \leqslant 0$
We know that the graphical representation of the given equation is given by
Fir let’s put (0, 0) in the given equation we get
$2\left( 0 \right) + 3\left( 0 \right) - 12 \leqslant 0$
$ \Rightarrow $$0 + 0 - 12 \leqslant 0$
$ \Rightarrow $$ - 12 \leqslant 0$
Since – 12 is less than 0 therefore the equation satisfies the statement
Hence, the region of the equation of line will be towards the origin

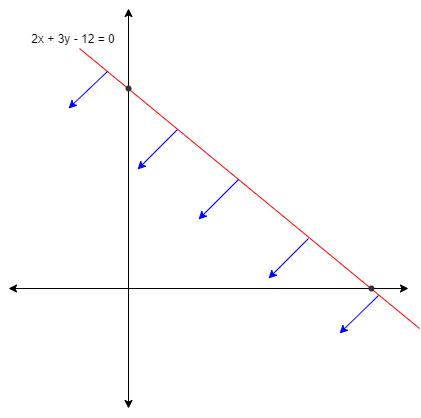
Now substituting the given points to check which of the points lie on the region of the equation.
For: (1, 2)
We get,
2 (1) + 3 (2) – 12 = 0
$ \Rightarrow $2 + 6 – 12 = 0
$ \Rightarrow $8 – 12 = 0
$ \Rightarrow $– 4 = 0
Since the result is negative it means the point lie on the region of the given line
For: (2, 1)
We get,
2 (2) + 3 (1) – 12 = 0
$ \Rightarrow $4 + 3 – 12 = 0
$ \Rightarrow $4 + 3 – 12 = 0
$ \Rightarrow $7 – 12 = 0
$ \Rightarrow $ – 5 = 0
Since the result is negative it means the point lie on the region of the given line
For: (2, 3)
We get,
2 (2) + 3 (3) – 12 = 0
$ \Rightarrow $4 + 9 – 12 = 0
$ \Rightarrow $1 = 0
Since the result is positive it means the point doesn’t lie on the region of the given line
For: (-3, 3)
We get,
2 (-3) + 3 (3) – 12 = 0
$ \Rightarrow $-6 + 9 – 12 = 0
$ \Rightarrow $- 9 = 0
Since the result is negative it means the point lie on the region of the given line
So, we know that accept (2, 3) every point lies on the region of the given line
Hence, (2, 3) is the point which doesn’t lie in the half plane.

So, the correct answer is “Option C”.

Note: In the above solution we came across the two terms “line” and “plane” where line can be defined as a straight figure which exists in one-dimension which have endless dimensions or a line is also the distance between the 2 points. Whereas a plane is constructed by the combination of two axis such as the combination of x axis and y axis will be x-y plane.