Question

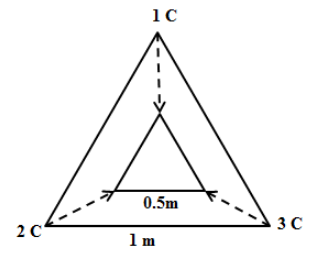
The point charges of 1 C, 2 C, and 3 C are placed at the corners of an equilateral triangle of side 1m. Calculate the work required to move these charges to the corners of a smaller equilateral triangle of side 0.5 m as shown.

Answer 1

Hint:Calculate the potential energy of the system of three charges placed at corners of a bigger equilateral triangle. Then calculate it when the charges are moved to a smaller triangle. The work done is equal to change in potential energy of the system of charges.

Formula used:
The potential energy between two point charges A and B is,
\[{U_{AB}} = k\dfrac{{{q_A}{q_B}}}{{r_{AB}^2}}\]
Here, k is constant, \[{q_A}\] is the charge of point charge A, \[{q_B}\] is the charge of point charge B, and \[{r_{AB}}\] is the distance between the charges A and B.
Work done is,
\[W = \Delta U\]
Here, \[\Delta U\] is the change in potential energy.

Complete step by step solution:
We have given the three charges, \[{q_1} = 1\,C\], \[{q_2} = 2\,C\] and \[{q_3} = 3\,C\]. These charges were initially at \[{r_1} = 1\,m\] from each other. We know that work done to move the charge from one point to another with reference to another charge is equal to change in the potential energy of the system of charges.Therefore, we can express the initial potential energy between system of three charges as follows,
\[{U_1} = k\left( {\dfrac{{{q_1}{q_2}}}{{{r_1}}} + \dfrac{{{q_2}{q_3}}}{{{r_1}}} + \dfrac{{{q_1}{q_3}}}{{{r_1}}}} \right)\]
\[ \Rightarrow {U_1} = \dfrac{k}{{{r_1}}}\left( {{q_1}{q_2} + {q_2}{q_3} + {q_1}{q_3}} \right)\]…… (1)
Here, k is the constant and it has value \[9 \times {10^9}\,{\text{N}}\,{{\text{m}}^2}/{{\text{C}}^{\text{2}}}\].
Now, we have given that these charges are moved to a smaller triangle such that the distance between each of them is \[{r_2} = 0.5\,m\]. We can express the potential energy of the system of charges as follows,
\[{U_2} = \dfrac{k}{{{r_2}}}\left( {{q_1}{q_2} + {q_2}{q_3} + {q_1}{q_3}} \right)\] …… (2)
Since the work done is equal to change in potential energy. We can write,
\[W = {U_2} - {U_1}\]
From equation (1) and (2), we have,
\[W = \dfrac{k}{{{r_2}}}\left( {{q_1}{q_2} + {q_2}{q_3} + {q_1}{q_3}} \right) - \dfrac{k}{{{r_1}}}\left( {{q_1}{q_2} + {q_2}{q_3} + {q_1}{q_3}} \right)\]
\[ \Rightarrow W = \left( {{q_1}{q_2} + {q_2}{q_3} + {q_1}{q_3}} \right)k\left( {\dfrac{1}{{{r_2}}} - \dfrac{1}{{{r_1}}}} \right)\]
Substituting \[{q_1} = 1\,C\], \[{q_2} = 2\,C\], \[{q_3} = 3\,C\], \[k = 9 \times {10^9}\,{\text{N }}{{\text{m}}^2}/{{\text{C}}^2}\], \[{r_2} = 1\,m\] and \[{r_1} = 0.5\,m\] in the above equation, we get,
\[W = \left( {\left( 1 \right)\left( 2 \right) + \left( 2 \right)\left( 3 \right) + \left( 1 \right)\left( 3 \right)} \right)\left( {9 \times {{10}^9}} \right)\left( {\dfrac{1}{{0.5}} - \dfrac{1}{1}} \right)\]
\[ \Rightarrow W = \left( {11} \right)\left( {9 \times {{10}^9}} \right)\left( 1 \right)\]
\[ \therefore W = 9.9 \times {10^{10}}\,{\text{J}}\]

Therefore, the work done for moving the charges to the smaller triangle is \[9.9 \times {10^{10}}\,{\text{J}}\].

Note:To determine the potential energy of the system of more than two charges, do not consider the product of all the charges in the numerator of equation (1). If you want to calculate the potential energy of point charges A, B and C, then add the potential energy of the point charges, A and B, then B and C, and then A and C.