Question

The plots of $\dfrac{1}{{{X_A}}}\;\rm{vs}\;\dfrac{1}{{{Y_A}}}$(where ${X_A}$and ${Y_A}$are the mole fraction of liquid $A$ in liquid and vapor respectively) is linear with slope and intercepts respectively.
(A) $P_A^0/P_B^0$ and $\dfrac{{(P_A^0 - P_B^0)}}{{P_B^0}}$
(B) $P_A^0/P_B^0$ and $\dfrac{{(P_B^0 - P_A^0)}}{{P_B^0}}$
(C) $P_B^0/P_A^0$ and $\dfrac{{(P_A^0 - P_B^0)}}{{P_B^0}}$
(D) $P_B^0/P_A^0$ and $\dfrac{{(P_B^0 - P_A^0)}}{{P_B^0}}$

Answer 1

Hint:
This question can be explained on the basis of Raoult’s law. The law states that partial pressure of each component of an ideal mixture of liquid is equal to the vapor pressure of pure components multiplied by its mole fraction.

Let liquid mixture has two components A and B.
Partial pressure of A is ${P_A} = P_A^0x_A$
Partial pressure of B is ${P_B} = P_B^0x_B$
$P_A^0 = $vapor pressure of liquid A.
$x_A = $mole fraction of A.
$P_B^0 = $vapor pressure of liquid B.
$x_B = $mole fraction of B.

Complete Step by Step Solution:
In the given equation:
$x_A = $mole fraction of A in liquid state
$y_A = $mole fraction of A in vapor phase
If we plot a graph of $\dfrac{1}{{x_A}}$vs $\dfrac{1}{{y_A}}$we get a straight line.

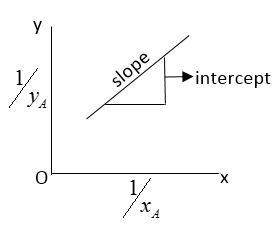
Let $P_A^0$be partial pressure of liquid A and $P_B^0$partial of vapor.
By Raoult’s law we have,
${P_A} = P_A^0x_A$_____ (1)
${P_B} = P_B^0x_B$_____ (2)
And $P_A^1 = {P_M}{Y_A}$and $P_B^1 = {P_m}{Y_B}$
$\therefore \dfrac{{{P_A}}}{{{Y_A}}} = \dfrac{{P_B^1}}{{{Y_B}}}$
$\Rightarrow \dfrac{{P_A^0x_A}}{{y_A}} = \dfrac{{P_B^0x_B}}{{y_B}} = \dfrac{{P_B^0(1 - x_A)}}{{(1 - y_A)}}$
As we know the sum of mole fraction of $x_A$and $x_B$is 1.
$x_A + x_B = 1$ and $y_A + y_B = 1$
 $\Rightarrow x_B - (1 - x_A)$
$\Rightarrow y_B - (1 - y_A)$

 $\Rightarrow \dfrac{{P_B^0}}{{x_A}} = \dfrac{{P_A^0}}{{y_A}} + (P_B^0 - P_A^0)$
$\Rightarrow \dfrac{1}{{x_A}} = \dfrac{1}{{y_A}}.\dfrac{{P_A^0}}{{P_B^0}} + \dfrac{{(P_B^0 - P_A^0)}}{{({P_B})}}$

Comparing above equation with $ y = mx + c$ we get
$y = \dfrac{1}{{{x_A}}}$
$x = \dfrac{1}{{{y_A}}}$
$m = \dfrac{{P_A^0}}{{P_B^0}}$
$c = \left( {\dfrac{{P_B^0 - P_A^0}}{{{P_B}}}} \right)$

Here, y and x are variable
$m = slope = \dfrac{{P_A^0}}{{P_B^0}}$
$c = \rm{intercept} = \left[ {\dfrac{{P_B^0 - P_A^0}}{{{P_B}}}} \right] $

Therefore, from the above explanation the correct option is (D) $P_B^0/P_A^0$ and $\dfrac{{(P_B^0 - P_A^0)}}{{P_B^0}}$

Raoult’s law is used to estimate the contribution of an individual component of a liquid or solid mixture to total pressure exerted by the system.

Note:
We should know that Raoult’s law is applicable to solutions containing non-volatile solute. It is not applicable for solute which dissociate or associate in the solution.