Question

The plane which bisects the line segment joining the points $\left( -3,-3,4 \right)$ and $\left( 3,7,6 \right)$at right angles, passes through which of the following points?
A. $\left( 4,1,7 \right)$
B. $\left( 4,1,-2 \right)$
C. $\left( 2,3,5 \right)$
D. $\left( 2,1,3 \right)$

Answer 1

Hint: To solve this question, we should know the properties of the plane in 3-D geometry. The midpoint C of the line segment joining the points $A\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ is given by $C\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2},\dfrac{{{z}_{1}}+{{z}_{2}}}{2} \right)$. We know that the required plane is bisecting the line joining the given points $A\left( -3,-3,4 \right)$, $B\left( 3,7,6 \right)$ and is perpendicular to the same line. So, we can infer that the line AB is the normal of the plane and the midpoint of AB is a point on the plane. The directional ratios of the line joining $A\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ are ${{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}}$. The equation of a plane whose directional ratios of the normal are $a,b,c$is $ax+by+cz=k$. We can substitute the midpoint in the equation of the plane and get the value of k. After getting the equation, we can substitute the points in the options and check which of them satisfy the equation of the plane.

Complete step-by-step answer:
We are given two points $A\left( -3,-3,4 \right)$, $B\left( 3,7,6 \right)$ and we are asked about the plane bisecting the line segment AB and perpendicular to AB.
We know that the midpoint C of the line segment joining the points $A\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ is given by $C\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2},\dfrac{{{z}_{1}}+{{z}_{2}}}{2} \right)$.
We can write the midpoint of the given line segment as
$C=\left( \dfrac{-3+3}{2},\dfrac{-3+7}{2},\dfrac{4+6}{2} \right)=\left( 0,2,5 \right)$

We know that the directional ratios of the line joining $A\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ are ${{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}}$.
The directional ratios of AB are
$\begin{align}
  & -3-3,-3-7,4-6 \\
 & \Rightarrow -6,-10,-2 \\
 & \Rightarrow 3,5,1 \\
\end{align}$
We know that the equation of a plane whose directional ratios of the normal are $a,b,c$is $ax+by+cz=k$.
We know that the line AB acts as a normal to the plane. So, we can conclude that the directional ratios of the line AB are the directional ratios of the normal of the required plane. We can write the equation of the required plane as
$3x+5y+z=k\to \left( 1 \right)$
We know that the point $C\left( 0,2,5 \right)$ lies on the plane in equation-1. By substituting in equation-1, we get
$\begin{align}
  & 3\times 0+5\times 2+5=k \\
 & \Rightarrow k=10+5=15 \\
\end{align}$
So, the required plane is
$3x+5y+z=15$
Let us consider point in option-A
$\left( 4,1,7 \right)$. Substituting in the equation of the plane, we get
$\begin{align}
  & 3\times 4+5\times 1+7=15 \\
 & 24=15 \\
\end{align}$
This is not true. So, option-A doesn’t lie on the plane.
Let us consider point in option-B
$\left( 4,1,-2 \right)$. Substituting in the equation of the plane, we get
$\begin{align}
  & 3\times 4+5\times 1+-2=15 \\
 & 15=15 \\
\end{align}$
This is true. So, option-B lies on the plane.
Let us consider point in option-C
$\left( 2,3,5 \right)$. Substituting in the equation of the plane, we get
$\begin{align}
  & 3\times 2+5\times 3+5=15 \\
 & 26=15 \\
\end{align}$
This is not true. So, option-C doesn’t lie on the plane.
Let us consider point in option-D
$\left( 2,1,3 \right)$. Substituting in the equation of the plane, we get
$\begin{align}
  & 3\times 2+5\times 1+3=15 \\
 & 14=15 \\
\end{align}$
This is not true. So, option-D doesn’t lie on the plane.
$\therefore $The point in option-B lies on the required plane $3x+5y+z=15$.

So, the correct answer is “Option B”.

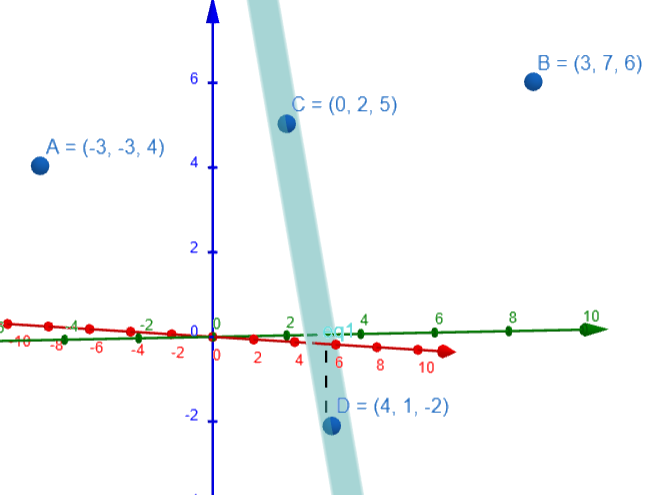
Note: We can see the diagram below and visualise the answer. The blue surface is the required plane $3x+5y+z=15$. The point C is the midpoint of the line AB and lies on the given plane. This question can have multiple answers but some students tend to stop after the answer of option-B. We have only a single answer in this question but there can be multiple answers and students should be careful while choosing the answer.