Question

The plane face of a plano convex lens is silvered. If \[\mu \] is the refractive index and \[r\] the radius of curvature of the curved surface, then the system behaves like a concave mirror of radius-
(A). \[\dfrac{r}{\mu }\]
(B). \[\dfrac{r}{\mu -1}\]
(C). \[r\mu \]
(D). \[r(\mu -1)\]

Answer 1

Hint: When a plano convex lens is silvered from one end, it acts as a mirror. The final image formation will take after the light ray undergoes reflection once from silvered surface and refraction twice on the lens surface. Using the formula for the combination of lens and mirror, we can calculate focus and use it to calculate radius of curvature of mirror.

Formula used:
 \[\dfrac{1}{{{f}_{s}}}=\dfrac{1}{{{f}_{m}}}+\dfrac{2}{{{f}_{l}}}\]
 \[\dfrac{1}{{{f}_{l}}}=(\mu -1)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]

Complete step by step solution:

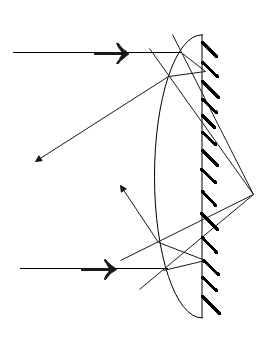
When lens and mirrors are in combination, the new focus is given by the formula-
 \[\dfrac{1}{{{f}_{s}}}=\dfrac{1}{{{f}_{m}}}+\dfrac{1}{{{f}_{l}}}+\dfrac{1}{{{f}_{l}}}\] [As the ray of light undergoes refraction twice on the surface of lens]
      \[\]
 \[\Rightarrow \dfrac{1}{{{f}_{s}}}=\dfrac{1}{{{f}_{m}}}+\dfrac{2}{{{f}_{l}}}\] - (1)
Here, \[{{f}_{s}}\] is the equivalent focus of lens and mirror combination
 \[{{f}_{m}}\] is the focus of mirror
 \[{{f}_{l}}\] is the focus of lens
As mirror is plane, \[R=\infty \] therefore \[{{f}_{m}}=\infty \] so, \[\dfrac{1}{{{f}_{m}}}=0\] .
For a lens,
 \[\dfrac{1}{{{f}_{l}}}=(\mu -1)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\] - (2)
Here,
 \[\mu \] is the refractive index
 \[{{R}_{1}}\] is the radius of first surface
 \[{{R}_{2}}\] is the radius of second surface
For lens of plano-convex lens, substituting values in eq (2), we get,
 \[\dfrac{1}{{{f}_{l}}}=(\mu -1)\left( \dfrac{1}{r} \right)\]
Substituting in eq (1), we get,
 \[\begin{align}
  & \dfrac{1}{{{f}_{s}}}=\dfrac{1}{{{f}_{m}}}+\dfrac{2}{{{f}_{l}}} \\
 & \dfrac{1}{{{f}_{s}}}=0+2\left( \dfrac{\mu -1}{r} \right) \\
 & \Rightarrow {{f}_{s}}=\dfrac{r}{2(\mu -1)} \\
\end{align}\]
 The focus of the resultant concave mirror is \[\dfrac{r}{2(\mu -1)}\] . We know, for a mirror, \[R=2f\]
Therefore, the radius of the resultant concave mirror will be-
 \[R=2\times \dfrac{r}{2(\mu -1)}=\dfrac{r}{(\mu -1)}\]
Radius of curvature is \[\dfrac{r}{(\mu -1)}\] .

So, the correct answer is “Option B”.

Note: Several combinations of lenses are possible like concavo-convex, convexo-concave, plano-concave, plano-convex etc. When one part of these lenses is silvered they act as mirrors. By convention, we take all the distances to the left as negative and all the distances to the right as positive.