Question

The place where angle of dip is 90 are known as
A. Geographical poles of the earth
B. Magnetic equator
C. Magnetic poles of earth
D. None of the above

Answer 1

Hint: The earth’s magnetic field at any given point on the magnetic meridian gets split up into two components, horizontal magnetic field of earth component $({{H}_{h}})$and the vertical magnetic field of earth component $({{H}_{v}})$. Each of these components, make an angle with the earth’s magnetic field, which will be required to solve the problem, $\cos \theta =\dfrac{{{H}_{h}}}{{{B}_{e}}}$. Here $\left( \theta \right)$is the angle of dip.

Complete answer:
Let’s start by discussing the geographic and magnetic meridians. Let’s consider a point on the earth’s surface. At this point, the direction of the circle made by the longitude determines the geographic North-South directions. That is the North-South poles of the earth. The geographic meridian is a vertical plane containing the longitudinal circle and the axis of the rotation of the earth.
In the same case, the magnetic meridian of a certain place can be defined as the vertical plane passing through an imaginary line passing through the magnetic north and the magnetic south poles. This plane intersects the surface of the earth in a longitude like a circle.
The earth’s magnetic field is $({{B}_{e}})$ and the horizontal and vertical components of the earth’s magnetic field are given by $({{H}_{h}})$ for the horizontal component and $({{H}_{v}})$ for the vertical component. Below is a diagram of the same.

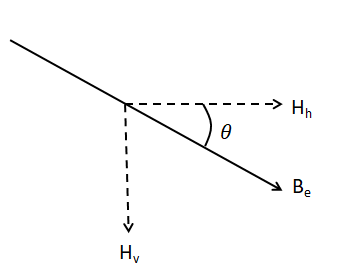
Given in the question is that, the horizontal component makes an angle of ${{90}^{0}}$. Therefore, \[\theta ={{90}^{0}}\] from the above diagram.
Therefore, taking the cosine of the angle, we get, $\cos \theta =\dfrac{{{H}_{h}}}{{{B}_{e}}}$. That is, $\cos ({{90}^{0}})=\dfrac{{{H}_{h}}}{{{B}_{e}}}\Rightarrow 0=\dfrac{{{H}_{h}}}{{{B}_{e}}}\Rightarrow {{H}_{h}}=0$. Therefore, the earth’s magnetic field is equal to the vertical components of the earth’s magnetic field, that is, ${{B}_{e}}={{H}_{h}}$. This occurs only at the magnetic north and south poles of earth, given by Option C.

Note:
Interestingly, this dip in the angle can be observed by us physically as well. If we can perfectly balance a magnetic needle about the horizontal axis, so that the magnetic needle is free to swing and align itself along the magnetic meridian, then the needle would make an angle with the horizontal axis. This angle is known as the angle of dip, which for the current problem was ${{90}^{0}}$.