
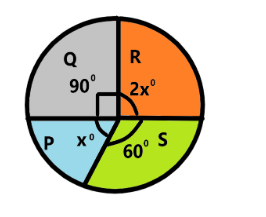
The pie chart shows the number of participants from four countries P, Q, R and S taking part in the tennis tournament. Given that there are 18 participants from country S, find the number of participants from country R.
A) 18
B) 21
C) 27
D) 42

Answer
558.9k+ views
Hint: The number of participants of respective countries are represented by the respective areas they cover in the given pie chart. All the line segments of the pie chart passes from the centre thus forming the sectors. To find the number of participants from country R, we need to find the area of sector R.
Area of sector:
$ A = \dfrac{\theta }{{360^\circ }} \times \pi {r^2} $ where, $ \theta $ is the angle formed by the sector at the centre and r is the radius of the circle.
Complete step by step solution:
The given pie chart of the four countries P, Q, R and S taking part in tennis tournament is:
As the pie chart is circular, the sum of all the angles will be equal to 360°. The given angles are 90°, 2x°, 60° and x°
\[
\Rightarrow 90^\circ + 60^\circ + x^\circ + 2x^\circ = 360^\circ \\
\Rightarrow 3x^\circ = 360^\circ - 90^\circ - 60^\circ \\
\Rightarrow 3x^\circ = 210^\circ \\
\Rightarrow x^\circ = \dfrac{{210^\circ }}{3} \\
\Rightarrow x^\circ = 70^\circ \\
\]
The angle formed in the sector representing country R is 2x°, substituting the value of x°, we get:
\[
2x^\circ = 2 \times 70^\circ \\
\Rightarrow 2x^\circ = 140^\circ \;
\]
The areas representing different countries are the areas of the sector of the circle formed as they are enclosed by the radius (in pie chart, the line segments are always drawn from the centre of the circle) and the adjoining arc.
The area of the sector of circle is given as:
$ A = \dfrac{\theta }{{360^\circ }} \times \pi {r^2}...(1) $ where, $ \theta $ is the angle formed by sector at the centre and r is the radius of the circle.
It is given that there are 18 participants from country S i.e. the area of sector S is equal to 18.
\[ \Rightarrow \dfrac{\theta }{{360^\circ }} \times \pi {r^2} = 18\] here,
Angle formed at the centre $ \left( \theta \right) $ = 60°
\[
\Rightarrow \dfrac{{60}}{{360}} \times \pi {r^2} = 18 \\
\Rightarrow\pi {r^2} = 18 \times 6 \\
\Rightarrow {r^2} = \dfrac{{18 \times 6}}{\pi }....(2) \;
\]
The value of the square of radius from the given information is calculated to be equal to $ \dfrac{{18 \times 6}}{\pi } $ .
Now, to find the number of participants from country R, we are supposed to find the area of the sector.
From (1):
$ A = \dfrac{\theta }{{360^\circ }} \times \pi {r^2} $ here,
Angle formed at the centre $ \left( \theta \right) $ = 140° (Calculated)
Substituting the value of $ {r^2} $ from (2), we get:
$
A = \dfrac{{140}}{{360}} \times \pi \times \dfrac{{18 \times 6}}{\pi } \\
\Rightarrow A = 42 ;
$
Therefore, the number of participants from country R in the tennis tournament is 42 and the correct option is D).
So, the correct answer is “Option D”.
Note: As the radius of the circle will not be changed from sector to sector, so we found its value from the given information and then substituted for calculation of area of sector R. we didn’t substitute the value of $ \pi $ while solving because it would have been cancelled later on and substituting the value would have increased the work
Area of sector:
$ A = \dfrac{\theta }{{360^\circ }} \times \pi {r^2} $ where, $ \theta $ is the angle formed by the sector at the centre and r is the radius of the circle.
Complete step by step solution:
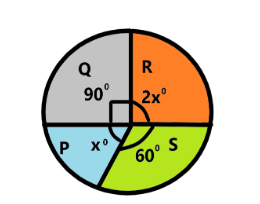
The given pie chart of the four countries P, Q, R and S taking part in tennis tournament is:

As the pie chart is circular, the sum of all the angles will be equal to 360°. The given angles are 90°, 2x°, 60° and x°
\[
\Rightarrow 90^\circ + 60^\circ + x^\circ + 2x^\circ = 360^\circ \\
\Rightarrow 3x^\circ = 360^\circ - 90^\circ - 60^\circ \\
\Rightarrow 3x^\circ = 210^\circ \\
\Rightarrow x^\circ = \dfrac{{210^\circ }}{3} \\
\Rightarrow x^\circ = 70^\circ \\
\]
The angle formed in the sector representing country R is 2x°, substituting the value of x°, we get:
\[
2x^\circ = 2 \times 70^\circ \\
\Rightarrow 2x^\circ = 140^\circ \;
\]
The areas representing different countries are the areas of the sector of the circle formed as they are enclosed by the radius (in pie chart, the line segments are always drawn from the centre of the circle) and the adjoining arc.
The area of the sector of circle is given as:
$ A = \dfrac{\theta }{{360^\circ }} \times \pi {r^2}...(1) $ where, $ \theta $ is the angle formed by sector at the centre and r is the radius of the circle.
It is given that there are 18 participants from country S i.e. the area of sector S is equal to 18.
\[ \Rightarrow \dfrac{\theta }{{360^\circ }} \times \pi {r^2} = 18\] here,
Angle formed at the centre $ \left( \theta \right) $ = 60°
\[
\Rightarrow \dfrac{{60}}{{360}} \times \pi {r^2} = 18 \\
\Rightarrow\pi {r^2} = 18 \times 6 \\
\Rightarrow {r^2} = \dfrac{{18 \times 6}}{\pi }....(2) \;
\]
The value of the square of radius from the given information is calculated to be equal to $ \dfrac{{18 \times 6}}{\pi } $ .
Now, to find the number of participants from country R, we are supposed to find the area of the sector.
From (1):
$ A = \dfrac{\theta }{{360^\circ }} \times \pi {r^2} $ here,
Angle formed at the centre $ \left( \theta \right) $ = 140° (Calculated)
Substituting the value of $ {r^2} $ from (2), we get:
$
A = \dfrac{{140}}{{360}} \times \pi \times \dfrac{{18 \times 6}}{\pi } \\
\Rightarrow A = 42 ;
$
Therefore, the number of participants from country R in the tennis tournament is 42 and the correct option is D).
So, the correct answer is “Option D”.
Note: As the radius of the circle will not be changed from sector to sector, so we found its value from the given information and then substituted for calculation of area of sector R. we didn’t substitute the value of $ \pi $ while solving because it would have been cancelled later on and substituting the value would have increased the work
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




