Question

The perpendicular from A on the side BC of a $\vartriangle ABC$ intersect BC at D such that DB = 3CD. Prove that $2A{B^2} = 2A{C^2} + B{C^2}$.

Answer 1

Hint: This problem requires the concept of triangles, and the Pythagoras theorem. We will begin by constructing a triangle according to the given data. The perpendicular AD which is formed divides the triangle into two right-angled triangles. We will apply the Pythagoras theorem to both the triangles to prove the given equation. The pythagoras theorem for a general right-angled triangle is given by-
${\left( {Base} \right)^2} + {\left( {Perpendicular} \right)^2} = {\left( {Hypotenuse} \right)^2}$
${B^2} + {P^2} = {H^2}$
Here, the hypotenuse is the longest side, opposite to the right angle.

Complete step-by-step answer:

We have been given a general triangle ABC. We have to construct a perpendicular through A, intersecting BC at a point D.

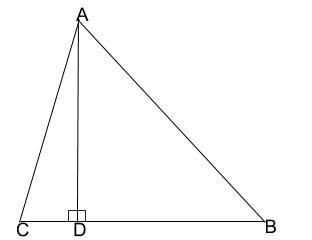
The perpendicular AD divides the figure into two right-angled triangles ADB and ADC, right-angled at D. Now that we have constructed the figure, we will try to prove the given equation. To do this, we will apply the Pythagoras theorem in triangles ADB and ADC, which is given by the formula-
 ${\left( {Base} \right)^2} + {\left( {Perpendicular} \right)^2} = {\left( {Hypotenuse} \right)^2}$
${B^2} + {P^2} = {H^2}$
Here, the hypotenuse is the longest side, opposite to the right angle.
$\begin{align}
  &In\;\vartriangle ADB,\; \\
  &{B^2} + {P^2} = {H^2} \\
  &D{B^2} + A{D^2} = A{B^2}...\left( 1 \right) \\
  &Similarly\;in\;\vartriangle ADC, \\
  &D{C^2} + A{D^2} = A{C^2}...\left( 2 \right) \\
\end{align} $
Now, we have also been given that DB = 3DC…(3)
We need to prove that $2A{B^2} = 2A{C^2} + B{C^2}$, so we need to eliminate the terms for AD, DB and DC in the equations. So, we will solve the equations as-
Substituting the value of DB from equation (3) in equation (1), we get-
$\begin{align}
  &D{B^2} + A{D^2} = A{B^2} \\
  &DB = 3DC \\
  &9D{C^2} + A{D^2} = A{B^2} \\
\end{align} $
We will subtract equation (2) from the above equation, to eliminate AD, as-
$\left( {9D{C^2} - D{C^2}} \right) + \left( {A{D^2} - A{D^2}} \right) = A{B^2} - A{C^2}$
$8D{C^2} + A{C^2} = A{B^2}...(4)$
Also, from the figure we know that-
DB + DC = BC
3DC + DC = BC
4DC = BC
$DC = \dfrac{{BC}}{4}...\left( 5 \right)$
Substituting the value of DC from equation (5) in equation (4), we get-
$\begin{align}
  &8{\left( {\dfrac{{BC}}{4}} \right)^2} + A{C^2} = A{B^2} \\
  &\dfrac{8}{{16}}B{C^2} + A{C^2} = A{B^2} \\
  &Multiplying\;both\;sides\;by\;2, \\
  &B{C^2} + 2A{C^2} = 2A{B^2} \\
  &2A{B^2} = B{C^2} + 2A{C^2} \\
\end{align} $
This is the required equation to be proved.
Hence, proved.

Note: In this question, solving the equation is a more important step than forming the equations. Most of the students form the equations by applying the Pythagoras theorem, but are unable to solve them further. Here, three equations can be formed easily, two by the theorem, and one relation is given(DB = 3CD). The fourth equation has to be formed by ourselves. This equation is DB + DC = BC, and is not given directly in the question. Students often forget to write this equation, and end up not being able to solve this question.