Question

The period of ${{\sin} ^ {2}} x$ is \[\]
A.$\dfrac{\pi} {2}$\[\]
B. $\pi $\[\]
C. $\dfrac{3\pi }{2}$\[\]
D. $2\pi $\[\]

Answer 1

Hint: We recall the definition of period and try find the minimum value positive value of $P$ such that ${{\sin }^{2}}\left( x+P \right)={{\sin }^{2}}x$. We use the formula ${{\sin }^{2}}\theta =\dfrac{1-\cos 2\theta }{2}$ , find all the solution of $\cos \theta =\cos \alpha $ that is $\theta =2n\pi +\alpha $and check for which value of $n$ we get minimum $P$, which will be the period.\[\]

Complete step-by-step solution:
We know from cosine double angle formula that for any acute angle $\theta $,
\[\begin{align}
 & \cos 2\theta =1-2{{\sin }^{2}}\theta \\
 & \Rightarrow {{\sin }^{2}}\theta =\dfrac{1-\cos 2\theta }{2}....\left( 1 \right) \\
\end{align}\]
We know that the solutions of the equation $\cos \theta =\cos \alpha $ are given by
\[\theta =2n\pi +\alpha ,n\in Z\]
We know that the period of a real valued function $f\left( x \right)$ is a nonzero positive constant $P$ for all $x$ in the domain of $f$ if
\[f\left( x+P \right)=f\left( x \right)\]
$P$ is also called the fundamental period or basic period. All the functional values of $f\left( x \right)$ will repeat after the interval of length $P$. The plot of periodic function exhibits translational symmetry which means the graph of function $f\left( x \right)$ is invariant in $x-$ axis with respect to translation by a length $P$. We can also writ for some positive integer $n$
\[f\left( x+nP \right)=f\left( x \right)\]
Here the given function is $f\left( x \right)={{\sin }^{2}}x$ where $f:{{R}^{+}}\bigcup \left\{ 0 \right\}\to {{R}^{+}}\bigcup \left\{ 0 \right\}$. Let us assume the period of ${{\sin }^{2}}x$ is $P$. So we have
\[{{\sin }^{2}}\left( x+P \right)={{\sin }^{2}}x\]
 We use relation (1) for $\theta =x+P,x$ and have
\[\begin{align}
  & \dfrac{1-\cos \left( 2\left( x+P \right) \right)}{2}=\dfrac{1-\cos 2x}{2} \\
 & \Rightarrow \cos \left( 2x+2P \right)=\cos 2x \\
\end{align}\]
The solutions of the above equation with some integer $n$ are
\[\begin{align}
  & 2x+2P=2x+2n\pi \\
 & \Rightarrow x+P=x+n\pi \\
 & \Rightarrow P=n\pi \\
\end{align}\]
The fundamental period is the minimum non-zero positive value of $P$ which we find with $n=1$ and hence the period of ${{\sin }^{2}}x$ is $P=1\times \pi =\pi $. So the correct option is C. If we plot $y={{\sin }^{2}}x$ then we can see the repeat of functional values after a period$\pi =3.14$.\[\]
 

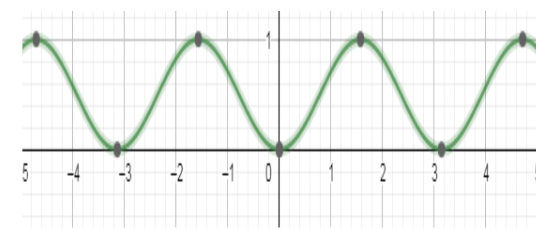
Note: We can alternatively solve by first finding the period of $\cos 2x$ using the fact that the period of $f\left( ax \right)$ is $\dfrac{P}{\left| a \right|}$. We then use the fact that the period of functions $f\left( x \right)$ and $g\left( x \right)$ are equal if and only if $f\left( x \right)=a+bg\left( x \right)$for ${{\sin }^{2}}x=\dfrac{1-\cos 2x}{2}$. If a function foes not have a period it is called aperiodic and if $f\left( x+T \right)=-f\left( x \right)$ then it is called anti-periodic.