Question

The perimeter of an isosceles triangle is 32cm. The ratio of the equal side to its base is 3:2 and the area of the triangle is $32\sqrt m $ $cm^2$. The value of m is

Answer 1

Hint: In this question, we use the concept of Heron's formula to find the area of a triangle and also use the perimeter of the isosceles triangle. Area of triangle by Heron’s formula $A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ , where $s = \dfrac{{a + b + c}}{2}$ and a, b and c are sides of triangle. Perimeter of the isosceles triangle is equal to the sum of all sides of the triangle.

Complete step-by-step solution -

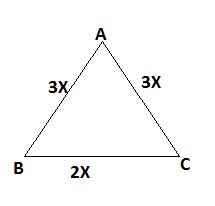
Consider an isosceles triangle $\vartriangle ABC$ in which AB=AC are equal sides and BC is a base.
Given, the perimeter of an isosceles triangle is 32cm and the ratio of the equal sides to its base is 3:2.
Let the equal sides of an isosceles triangle is 3x and the base is 2x.
So, AB=AC=3x and BC=2x
Now, the perimeter of an isosceles triangle is 32cm.
$
  AB + BC + AC = 32 \\
   \Rightarrow 3x + 2x + 3x = 32 \\
   \Rightarrow 8x = 32 \\
   \Rightarrow x = 4cm \\
 $
So, the equal sides of an isosceles triangle is $3x = 3 \times 4 = 12cm$ and base is $2x = 2 \times 4 = 8cm$ .
AB=AC=12cm and BC=8cm.
Now, to find the area of the triangle we have to use Heron’s formula.
$A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ , where $s = \dfrac{{a + b + c}}{2}$ and a=8cm , b=12cm , c=12cm.
$
   \Rightarrow s = \dfrac{{8 + 12 + 12}}{2} = \dfrac{{32}}{2} \\
   \Rightarrow s = 16 \\
 $
Area of triangle, $A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
$
   \Rightarrow A = \sqrt {16\left( {16 - 8} \right)\left( {16 - 12} \right)\left( {16 - 12} \right)} \\
   \Rightarrow A = \sqrt {16 \times 8 \times 4 \times 4} \\
   \Rightarrow A = \sqrt {16 \times 4 \times 2 \times 16} \\
   \Rightarrow A = 16 \times 2\sqrt 2 \\
   \Rightarrow A = 32\sqrt 2 c{m^2} \\
 $
Also given that the area of the triangle is $32\sqrt m $ $cm^2$.
Now, comparing both the areas.
$
   \Rightarrow 32\sqrt m = 32\sqrt 2 \\
   \Rightarrow m = 2 \\
 $
So, the value of m is 2.

Note: Whenever we face such types of problems we use some important points. First we find the length of sides of an isosceles triangle by using the ratio of sides and perimeter of the triangle mentioned in the question and then find the area of the triangle by using Heron's formula. Then we have to compare both areas of the triangle.