Question

The percentage change in the acceleration of the earth towards the Sun from a total eclipse of the Sun to the point where the moon is on a side of earth directly opposite to the sun is?
\[\begin{align}
  & \text{A) }\dfrac{{{M}_{S}}}{{{M}_{M}}}\dfrac{{{r}_{2}}}{{{r}_{1}}}\times 100 \\
 & \text{B) }\dfrac{{{M}_{S}}}{{{M}_{M}}}{{(\dfrac{{{r}_{2}}}{{{r}_{1}}})}^{2}}\times 100 \\
 & \text{C) 2(}\dfrac{{{r}_{1}}}{{{r}_{2}}}{{)}^{2}}\dfrac{{{M}_{M}}}{{{M}_{S}}}\times 100 \\
 & \text{D) (}\dfrac{{{r}_{1}}}{{{r}_{2}}}{{)}^{2}}\dfrac{{{M}_{M}}}{{{M}_{S}}}\times 100 \\
\end{align}\]

Answer 1

Hint: We need to relate the effect of the moon in the path between the gravitational field of the sun and the earth during an eclipse. The distance dependence also needs to be taken into consideration to find the required percentage.

Complete step by step solution:
The gravitational force of attraction on a body is dependent on the masses of the body between which the force is considered. The force of attraction is given by the Newton’s Gravitational law as –
\[F=\dfrac{GMm}{{{R}^{2}}}\]
Where, M and m are the masses of the bodies,
R is the radial distance between the two bodies,
G is the gravitational constant.
During an eclipse, all the three bodies – sun, moon and earth come in a straight line.

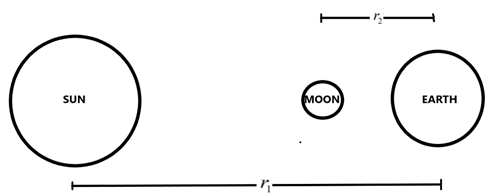
The total gravitational force acting on the earth will be the sum of the forces due to the sun and the moon. It is given as –
\[{{F}_{total}}=\dfrac{G{{M}_{S}}{{m}_{e}}}{{{r}_{1}}^{2}}+\dfrac{G{{M}_{M}}{{m}_{e}}}{{{r}_{2}}^{2}}\]
When the moon is at the opposite side of the earth, then the effective force acting on earth will be given as the difference between forces due to the sun and the moon.

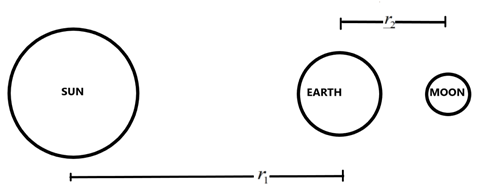
It is given as –
\[{{F}_{eff}}=\dfrac{G{{M}_{S}}{{m}_{e}}}{{{r}_{1}}^{2}}-\dfrac{G{{M}_{M}}{{m}_{e}}}{{{r}_{2}}^{2}}\]
Now, we can find the change in force experienced by earth during these two situations by finding the difference between the two above forces as –
\[\begin{align}
  & \Delta F={{F}_{total}}-{{F}_{eff}} \\
 & \Rightarrow \Delta F=\dfrac{G{{M}_{S}}{{m}_{e}}}{{{r}_{1}}^{2}}+\dfrac{G{{M}_{M}}{{m}_{e}}}{{{r}_{2}}^{2}}-\{\dfrac{G{{M}_{S}}{{m}_{e}}}{{{r}_{1}}^{2}}-\dfrac{G{{M}_{M}}{{m}_{e}}}{{{r}_{2}}^{2}}\} \\
 & \therefore \Delta F=2\dfrac{G{{M}_{M}}{{m}_{e}}}{{{r}_{2}}^{2}} \\
\end{align}\]
Now, we can find the change in acceleration of the earth due to the change in force –
\[\begin{align}
  & \Delta F=2\dfrac{G{{M}_{M}}{{m}_{e}}}{{{r}_{2}}^{2}} \\
 & \Rightarrow \Delta a=\dfrac{\Delta F}{{{m}_{e}}} \\
 & \therefore \Delta a=2\dfrac{G{{M}_{M}}}{{{r}_{2}}^{2}} \\
\end{align}\]
Now, we know the acceleration of the earth due to the average force acting on the earth by finding the average of the total force and the effective force on the earth as –
\[\begin{align}
  & F=\dfrac{{{F}_{total}}+{{F}_{eff}}}{2} \\
 & \Rightarrow F=\dfrac{\dfrac{G{{M}_{S}}{{m}_{e}}}{{{r}_{1}}^{2}}+\dfrac{G{{M}_{M}}{{m}_{e}}}{{{r}_{2}}^{2}}+\{\dfrac{G{{M}_{S}}{{m}_{e}}}{{{r}_{1}}^{2}}-\dfrac{G{{M}_{M}}{{m}_{e}}}{{{r}_{2}}^{2}}\}}{2} \\
 & \Rightarrow F=\dfrac{G{{M}_{S}}{{m}_{e}}}{{{r}_{1}}^{2}} \\
 & a=\dfrac{F}{{{m}_{e}}} \\
 & \therefore a=\dfrac{G{{M}_{S}}}{{{r}_{1}}^{2}} \\
\end{align}\]
Now, we can find the change in the acceleration as –
\[\begin{align}
  & \dfrac{\Delta a}{a}\times 100=\dfrac{2\dfrac{G{{M}_{M}}}{{{r}_{2}}^{2}}}{\dfrac{G{{M}_{S}}}{{{r}_{1}}^{2}}}\times 100 \\
 & \therefore \dfrac{\Delta a}{a}\times 100=2\dfrac{{{M}_{M}}}{{{M}_{S}}}{{(\dfrac{{{r}_{1}}}{{{r}_{2}}})}^{2}}\times 100 \\
\end{align}\]
This is the required solution for the percentage change in acceleration.

The correct answer is option C.

Note:
The gravitational force experienced by a celestial object in the solar system is dependent on the large massive planets, asteroids and the sun. The gravitational force decreases by the square of the distance but can still have an effect due to the large mass