Question

The order of the rotational symmetry of the parallelogram about the centre is
A.0
B.1
C.2
D.3

Answer 1

Hint: We know the definition of rotational symmetry. The order of rotational symmetry of a shape is the number of times you can rotate a shape so that it looks the same. We include the original position but only once, i.e., not when it returns to its original position. We draw the diagram of parallelogram and rotate it about the centre and we find the order of symmetry.

Complete step-by-step answer:
We know that in parallelograms opposite sides are congruent (equal).
See the diagram.

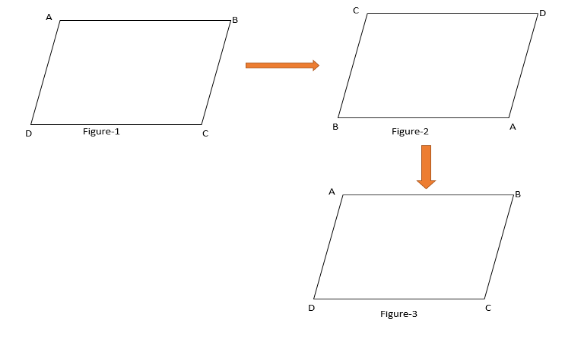
Figure-1 is our original parallelogram. Let’s rotate the figure-1 about the centre through \[{180^0}\]clockwise direction. We obtain the figure-2 which has the same shape as our original parallelogram figure one. Now, let’s rotate the figure-2 about the centre through \[{180^0}\] clockwise direction. We obtain the figure-3 which is the same as figure-1 that is our original parallelogram.
We include the original position but only once, hence the order of the rotational symmetry of the parallelogram about the centre is $2$.
So, the correct answer is “Option C”.

Note: If we rotate the above diagram about the centre through \[{90^0}\], we don’t obtain the same shape as the original. This goes the same for \[{270^0}\]. In the order of rotational symmetry we only care about the shape and the vertices (vertices may differ, see in above diagram). Remember the important note that we include the original position but only once, i.e., not when it returns to its original position.