Question

The number of three digit numbers having no digits as $5$ is
$
  {\text{A}}{\text{. 252}} \\
  {\text{B}}{\text{. 225}} \\
  {\text{C}}{\text{. 648}} \\
  {\text{D}}{\text{. none of these}} \\
 $

Answer 1

Hint: This problem is based on the principle of fundamental counting which states that if there are n ways of doing something, and m ways of doing another thing after that, then there are $m \times n$ ways to perform both of these actions.

Complete step-by-step answer:
We know that
 A three digit number has three places Ones, tenths and hundredths. Each place can be filled with any number between \[0{\text{ to 9}}\] .
For a three digit number without$5$ , hundreds place can be filled with any number except $0{\text{ and 5}}{\text{.}}$
Therefore the number of digits that can be placed at the hundredth’s place is $8$ .
Number 5 cannot be used as mentioned in the question.
So, number of digits that can be placed in tenth’s place is $9.$
And, number of digits that can be placed in one’s place is $9.$

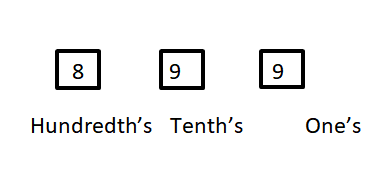
So, from the principle of fundamental counting number of three digit numbers having no digits as $5$ is
$
   = 8 \times 9 \times 9 \\
   = 648 \\
 $
Hence, the number of three digits numbers having no digits as \[5{\text{ is 648}}{\text{.}}\]

Note: This problem is based on fundamental counting principle and for similar problems like this we have to find the number of ways a task can be done. These types of problems exclude the way which is not required and count the others left. In a three digit number zero cannot be placed at the hundredth’s place because the number will no longer be a three digit number.