
The number of real solutions of the equation $ {x^2} = 1 - \left| {x - 5} \right| $ is
A. $ 1 $
B. $ 2 $
C. $ 4 $
D. No solution
Answer
529.5k+ views
Hint: Here, we will find the points of the intersection of the curves by taking both the sides of the equation as any variable such as “y”. Then the number of the real solutions of the equation is equal to the number of points of the intersection of two curves.
Complete step by step solution:
Take the given expression: $ {x^2} = 1 - \left| {x - 5} \right| $
Take both the sides of the equation as the term “y”.
Therefore, $ y = {x^2} $ and $ y = 1 - \left| {x - 5} \right| $
Now, draw the graph using the above two expressions.
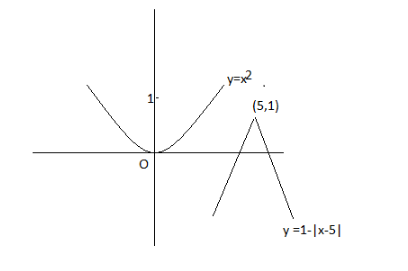
We can observe that since the above two graphs do not intersect each other. The solution for the given expression does not exist.
Hence, from the given multiple choices, the option D is the correct answer.
So, the correct answer is “Option D”.
Note: Always observe the given expression and then decide how to proceed for the solution. Since, here we were asked to find the number of points of the intersection we used a graph method but at times you can proceed finding the factors of the expression.
Scale the graph as per the given data. Always take the appropriate units as the scale to have a clear pictorial and presentable graph which can give us the exact data and which can be easily compared among the given parameters. Also, refer to the other types of the graphs and know the difference between them and the pictorial representation or the diagram which represents the data or the value in the most organized manner. There are different types of graphs such as bar graph, line graph, pie chart and bubble and radar graph.
Complete step by step solution:
Take the given expression: $ {x^2} = 1 - \left| {x - 5} \right| $
Take both the sides of the equation as the term “y”.
Therefore, $ y = {x^2} $ and $ y = 1 - \left| {x - 5} \right| $
Now, draw the graph using the above two expressions.
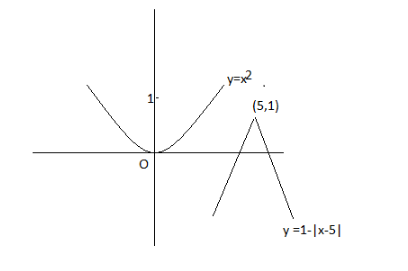
We can observe that since the above two graphs do not intersect each other. The solution for the given expression does not exist.
Hence, from the given multiple choices, the option D is the correct answer.
So, the correct answer is “Option D”.
Note: Always observe the given expression and then decide how to proceed for the solution. Since, here we were asked to find the number of points of the intersection we used a graph method but at times you can proceed finding the factors of the expression.
Scale the graph as per the given data. Always take the appropriate units as the scale to have a clear pictorial and presentable graph which can give us the exact data and which can be easily compared among the given parameters. Also, refer to the other types of the graphs and know the difference between them and the pictorial representation or the diagram which represents the data or the value in the most organized manner. There are different types of graphs such as bar graph, line graph, pie chart and bubble and radar graph.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW





