Question

The number of lines of symmetry in a divider is:
A. 0
B. 1
C. 2
D. 3

Answer 1

Hint: For solving this question you should know about the symmetry lines for any shape. In this problem first we will discuss the symmetricity for the alphabets and see the examples. And then we will see the symmetricity in a divider.

Complete step by step answer:
According to the question it is asked to us to find the number of lines of symmetry in a divider. So, as we know that the vertical shapes are the same in mirror image also. For understanding the symmetricity we see some examples of English alphabets.
If we take the example of A and B, then,

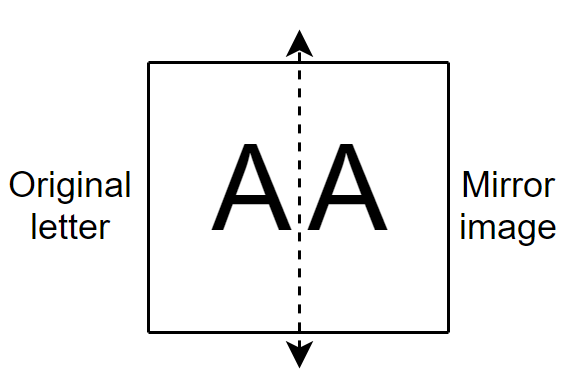
So, the mirror image of A is the same as of the original or real letter A.
Now we make the mirror image of B, so then,

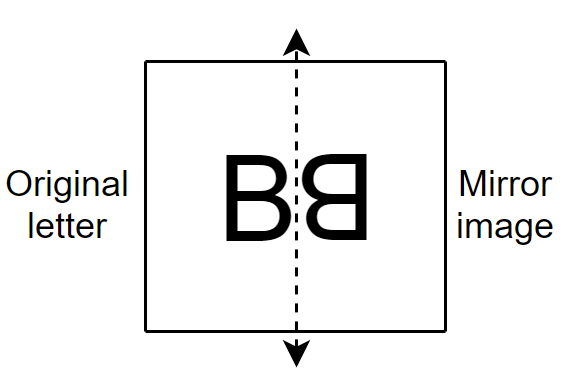
The mirror image of B is not symmetric, because both are looking different and looking the opposite of each other.
To solve these questions the concept of alphabet reflection symmetry is used and that states that the letters are written from right to left and they appear as they are written from left to right in the mirror image. The letters like A, M and U, T, O or many other letters are the same as the original letter in the mirror image. Like as these if we see in the mirror to H, I,M, O, U, T, V, W, X, Y these all letters are also appearing the same as real letters.
Now if we take our question, then shape of a divider is,

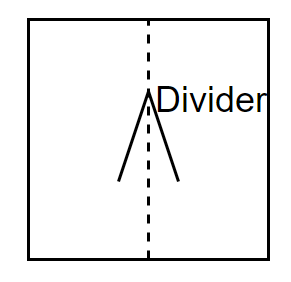
As we can see here only one line of symmetry is available.
So, the correct answer is “Option B”.

Note: For solving this type of questions we should know that according to the concept of symmetry of alphabet reflection if any letter’s reflection is as same in looking and size etc, as the real letter, then the reflection is symmetric. And apply the same concept on other materials also.