Question

The number of geometric isomers possible for the complex:
${[Co{L_2}C{l_2}]^ - }(L = {H_2}NC{H_2}C{H_2}{O^ - })$ is

Answer 1

Hint:The complex is unsymmetrical bidentate ligand. For a complex, there are two possible isomers either the A ligands can be adjacent to one another (cis) and the B ligands must also be cis, or the A ligands can be across from one another (trans), in which case the B ligands must also be trans.

Complete answer:
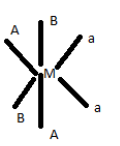
Metal complexes that differ only in which ligands are adjacent to one another (cis) or directly across from one another (trans) in the coordination sphere of the metal are called geometrical isomers. General form of the complex is $[M{(AB)_2}{a_2}]$. If the complex contains a bidentate ligand, the ends of that ligand must occupy cis sites around the square planar.
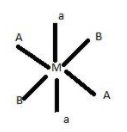
The complex $[M{(AB)_2}{a_2}]$ will passes two geometrical isomer (Cis and trans) in which two different ligand are present and its Cis isomer is optically active in contrast to trans form. Being a bidendate ligand attached to it, both the ligand will have their respective cis and tras form.
Therefore for the two different ligand cis and trans from along with active cis optically active isomers 5 different geometric isomers wil be formed.

Therefore the correct answer is 5.

The five different geometric isomers are :
1.

2.

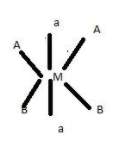
3.

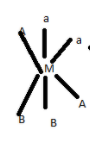
4.

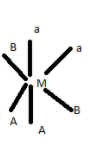
5.

Note:
Many metal complexes form isomers, which are two or more compounds with the same formula but different arrangements of atoms. Structural isomers differ in which atoms are bonded to one another, while geometrical isomers differ only in the arrangement of ligands around the metal ion. Ligands adjacent to one another are cis, while ligands across from one another are trans.