Question

The number of different garlands, that can be formed using 3 flowers of the first kind and 3 flowers of the second kind, is
A. 60
B. 20
C. 4
D. 3

Answer 1

Hint: The garland is in the shape of a circle. So, first, we will set the first kind of flower that is 3 flowers in a circular shape. Then we will have 3-second kinds of flowers which we will have to set in between the 3 first kinds of flowers. For that, we have the formula that number of ways in which r things can be set in between n things that are,
${}^{n+r-1}{{C}_{r-1}}$
And if the objects set in a circular way then the number of ways are,
${}^{n+r-1}{{C}_{r-1}}\left( n-1 \right)!$

Complete step-by-step answer:
The figure is shown below:

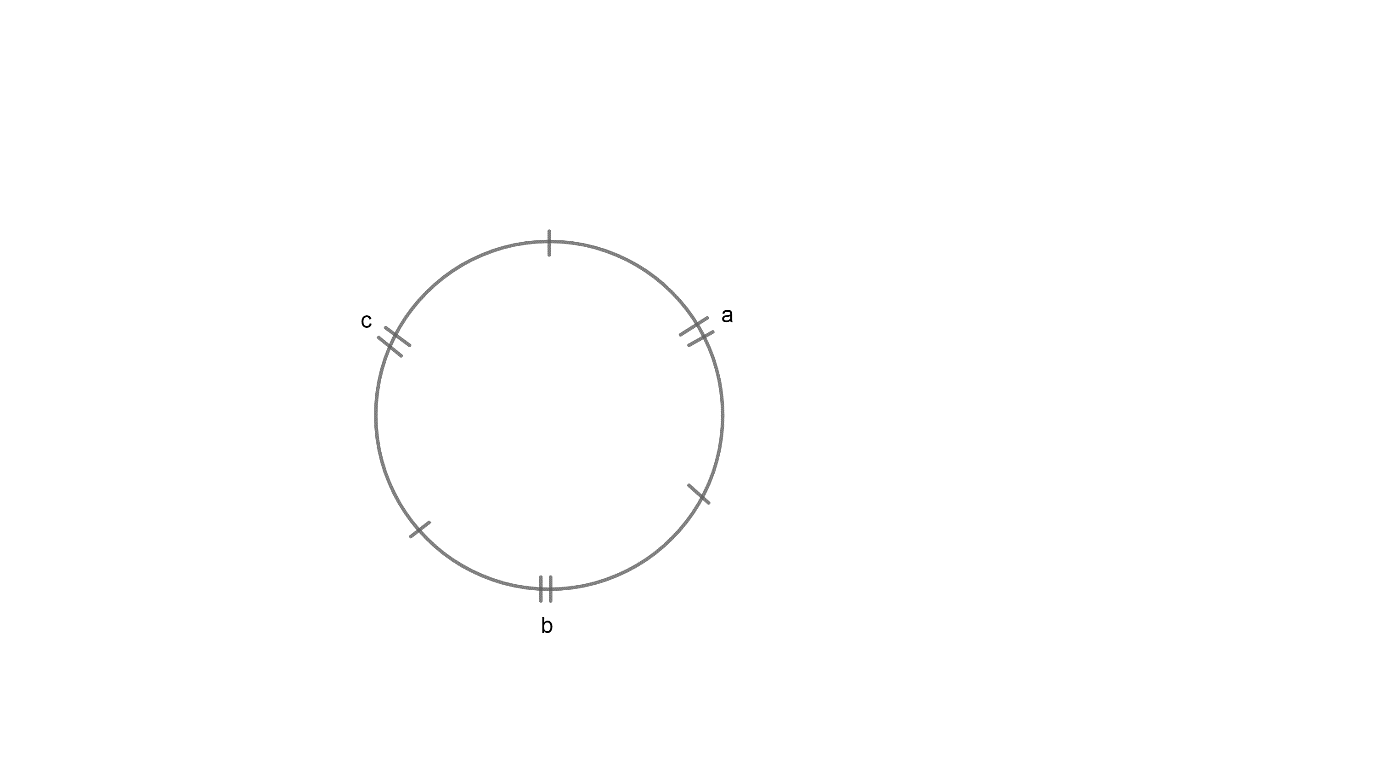
First, we will set the first kind of flower in a circular way. Then we will have set a, b, c (second kind of flowers) which will set in between the first kind.
As $a+b+c=3$ and a, b, c can be zero, one, two, and three.
The total number of ways are given by,
${}^{n+r-1}{{C}_{r-1}}\left( n-1 \right)!$
Applying formula and,
$\begin{align}
  & n=3 \\
 & r=3 \\
\end{align}$
We have the total number of ways to make different garlands.
$\begin{align}
  & ={}^{3+3-1}{{C}_{3-1}}\left( 3-1 \right)! \\
 & ={}^{5}{{C}_{2}}\left( 2 \right)! \\
 & =\dfrac{5!}{2!3!}\times 2! \\
 & =\dfrac{5!}{3!} \\
 & =\dfrac{5\times 4\times 3!}{3!} \\
 & =20 \\
\end{align}$
So, the total number of ways are 20.

Note: As first we arrange all the first kind of flowers than for arranging the second kind of flowers, students might think that each flower of the second kind is there in between two flowers of the first kind as shown in the figure.

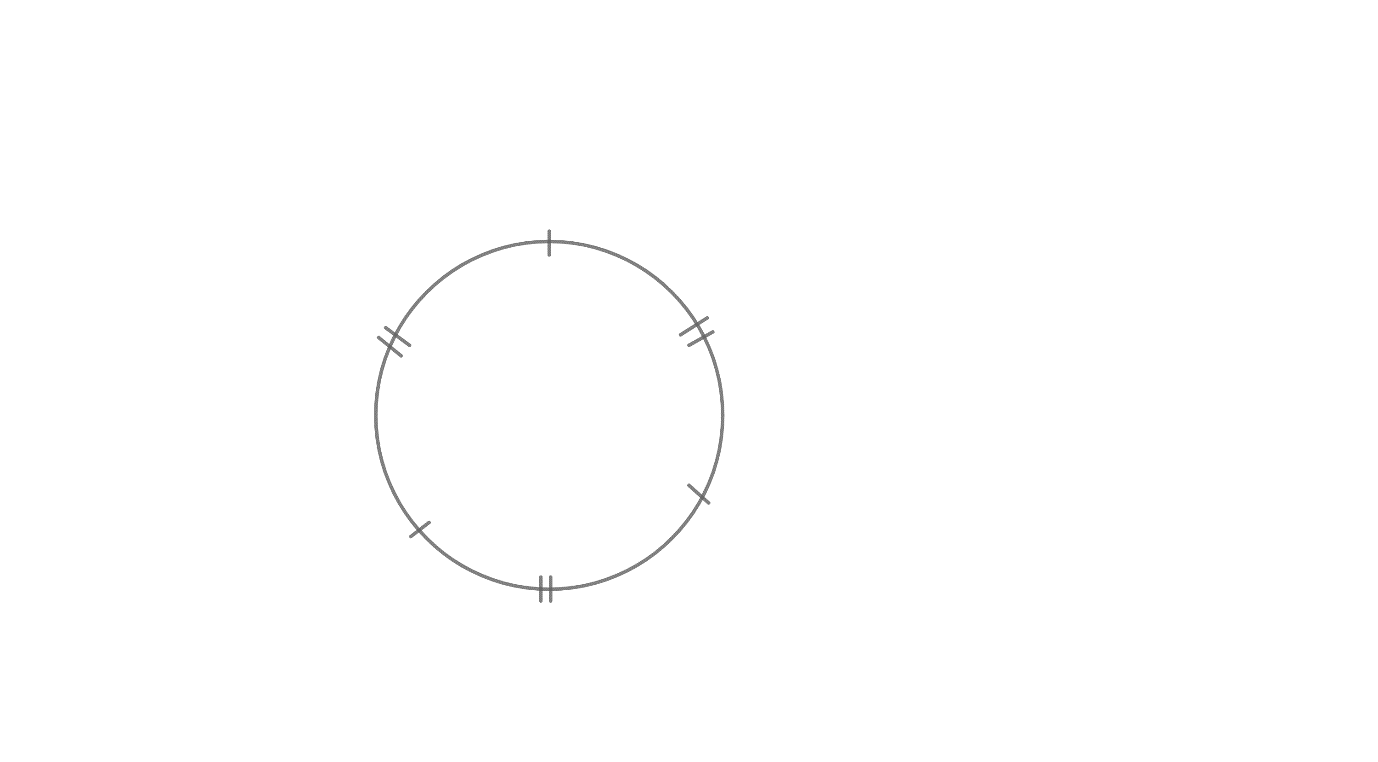
This is wrong as there is only one possibility. But as we have to find all the possible ways to arrange the garland. So, there can be zero, one, two, or three flowers in between two flowers of the first kind.