Question

The north poles of pole strengths m, 9m are kept apart by a certain distance. Find the distance of the full point from the larger pole.
A. $\dfrac{{3d}}{4}$
B. $\dfrac{{3d}}{8}$
C. $\dfrac{{3d}}{{16}}$
D. $\dfrac{{3d}}{2}$

Answer 1

Hint: This problem can be solved by direction application of the Biot-Savart’s law to calculate the magnetic field at a particular point between the two points. At this particular point, the magnetic field exerted by both the poles will be equal and hence, cancel out each other. This is termed as the full point from the larger pole.

Complete step-by-step answer:
Biot Savart’s law gives us an insight about the term magnetic field that arises due to presence of electric current.
Consider a line element in a conductor $dl$ through which current is flowing and an arbitrary point P at a distance of r from the conductor

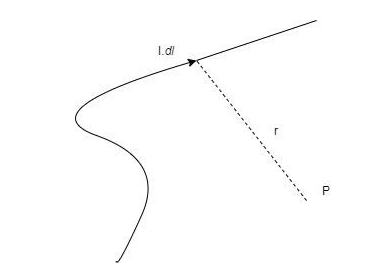
It states that, the magnetic field due to the line element $dl$is given by –
$dB \propto \dfrac{{I.dl}}{{{r^3}}}$
By removing the proportionality symbol, we have –
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I.dl}}{{{r^3}}}$ where ${\mu _0}$ is called the absolute permeability.
For an straight line, to obtain the field, we have to integrate the equation w.r.t length
\[
  \int\limits_l {dB} = \dfrac{{{\mu _0}I}}{{4\pi }}\int {\dfrac{{dl}}{{{r^3}}}} \\
  Integrating, \\
  B = \dfrac{{{\mu _0}I}}{{4\pi }}\left[ {\dfrac{2}{{{r^2}}}} \right] \\
   \to B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{{{r^2}}} \\
 \]
Consider the poles separated by a distance d.

Let x be the distance of the null point where the field by the two poles will be equal.
${B_1} = {B_2}$
Substituting, we get –
$\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 9m}}{{{x^2}}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times m}}{{{{\left( {d - x} \right)}^2}}}$
Rearranging, we get –
\[
  \dfrac{{{x^2}}}{{{{\left( {d - x} \right)}^2}}} = \dfrac{{2 \times 9m}}{{2m}} \\
   \to {\left( {\dfrac{x}{{d - x}}} \right)^2} = 9 \\
   \to \dfrac{x}{{d - x}} = \sqrt 9 = 3 \\
   \to x = 3\left( {d - x} \right) \\
   \to x = 3d - 3x \\
   \to x + 3x = 3d \\
   \to 4x = 3d \\
   \to x = \dfrac{{3d}}{4} \\
 \]
Hence, the distance of the null point, $x = \dfrac{{3d}}{4}$

Hence, the correct option is Option A.

Note: Applying Biot-Savart’s Law and another law called Ampere’s Circuital law for any condition will result in the same expression for the magnetic field. The Ampere’s law is, however, very significant in electromagnetic radiation, wherein, a scientist by name James Maxwell, generalised this Ampere’s law equation to include in the list of his 4 fundamental Maxwell equations of classical electromagnetism.
The term ${\mu _0}$ in the expression for the Biot-Savart’s law is called absolute permeability. It is a quantity which represents the degree to which the material can allow the magnetic lines to pass through the material.