Question

The molecular electronic configuration of \[B{e_2}\]is:
A. \[\sigma 1{s^2},\sigma *1{s^2},\sigma 2{s^2},\sigma *2{p^2}\]
B. \[\sigma 1{s^2},\sigma 2{s^2}\]
C. \[\sigma 1{s^2},\sigma *1{s^2},\sigma 2{s^2},\sigma *2{s^2}\]
D. None of the above

Answer 1

Hint: We have to remember that the electron configuration is the distribution of electrons of an atom or molecule in atomic or molecular orbitals. In order to proceed with the molecular electronic configuration, we first need to know the number of electrons in \[B{e_2}\]. Atomic number of $Be$ is $4$, hence the total number of electrons in \[B{e_2}\] is $8$. We also need to understand molecular orbitals and molecular orbital theory to be able to write the molecular electronic configuration of any molecule.

Complete step by step answer:
To begin understanding molecular orbitals, we have to first consider atomic orbitals. Let us consider the example of the simplest atom-hydrogen. We have to remember that the chemical bond is formed by the combination of two atomic orbitals.
The simplest way to obtain a molecular electronic configuration is to draw a molecular orbital diagram. Molecular orbital diagram is a plot of atomic orbitals and molecular orbitals with respect to energy. Energy is plotted vertically. The orbital with higher energy is less stable while lower energy is more stable.
In the similar way, the molecular electronic configuration of \[B{e_2}\] can be determined using molecular orbital diagram as follows:

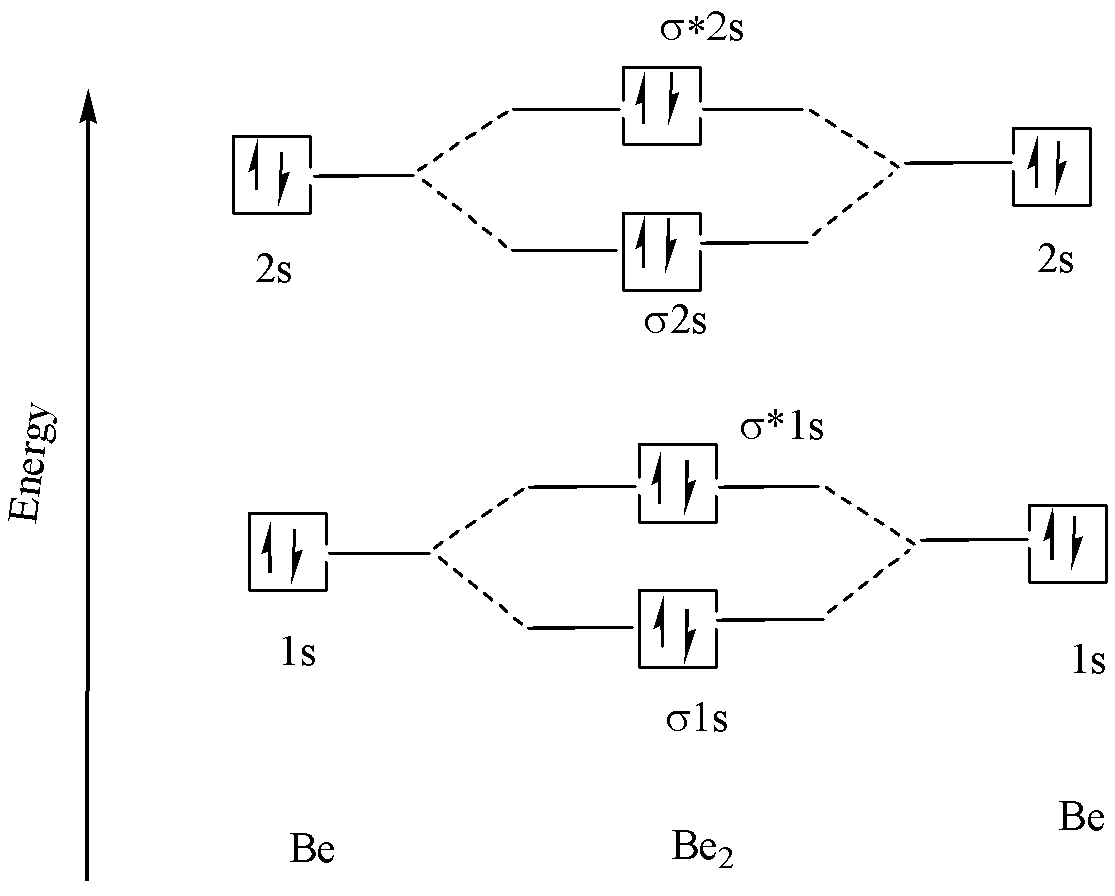
No. Of electrons in Be atom = \[4\]
Electronic configuration of Be atom = \[1{s^2}2{s^2}\]
No. Of electrons in \[B{e_2}\] molecule = $8$
Molecular electronic configuration of \[B{e_2}\] molecule = \[\sigma 1{s^2},\sigma *1{s^2},\sigma 2{s^2},\sigma *2{s^2}\].
We can calculate the bond order of beryllium using the formula as,
Bond order $ = \dfrac{1}{2}\left[ {{N_b} - {N_a}} \right]$
$ \Rightarrow {\text{Bond order}} = \dfrac{1}{2}\left[ {2 - 2} \right] = 0$

So, the correct answer is Option C.

Note: It must be noted that just as atomic orbitals are distinguished as s, p, d, and f orbitals and determined by quantum numbers. Molecular orbitals are also determined by quantum numbers and we have σ,π and δ orbitals. Molecular orbitals obey the following rules just as atomic orbitals. (a) Pauli’s Exclusion Principle: No two electrons in an atom have the same four quantum numbers. (b) Hund’s rule of maximum multiplicity: Orbitals having the same energy level should have one electron each before pairing takes place.