Question

The measure of two adjacent angles of a parallelogram are in the ratio $3:2$ .Find the measure of smallest of the angles of the parallelogram(in degree).

Answer 1

Hint: First, we should know the property of parallelogram i.e. summation of all the angles is $360{}^\circ $ and summation of adjacent angles is $180{}^\circ $ . From this, we have to assume any angle as 3x and angle adjacent to it as 2x. Then on adding and equating it with 180 i.e. $3x+2x=180{}^\circ $ we can find the value of x. After finding the value of x, we will put that in 3x and 2x and then compare which value of angle is smaller.

Complete step-by-step answer:
In the question, we are given a ratio of two adjacent angles as $3:2$ . So, first we will draw a figure for clear understanding.

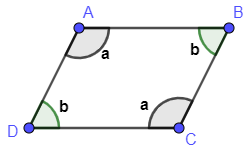
As we can see in the diagram that $\angle A=\angle C=a$ and $\angle B=\angle D=b$ so, opposite angles are the same.
Here, we should know the property of parallelogram that summation of all the angles is $360{}^\circ $ and summation of adjacent angles is $180{}^\circ $ .
We are given a ratio of two adjacent angles which we can consider as $\angle A=3x$ and $\angle B=2x$ . So, we can write it as
$\angle A+\angle B=180{}^\circ $
On substituting the values, we get
$3x+2x=180{}^\circ $
$5x=180{}^\circ $
So, we will divide LHS and RHS by 5 and we will get as
$x=\dfrac{180{}^\circ }{5}=36{}^\circ $ ………………………..(1)
Now, we will find value of angle A and B as
$\angle A=3x=3\times 36=108{}^\circ $
$\angle B=2x=2\times 36=72{}^\circ $
Therefore, $\angle B=\angle D=72{}^\circ $ and $\angle A=\angle C=108{}^\circ $ .
Thus, the smallest angle in parallelogram is $72{}^\circ $ .

Note: Always remember to do verification for such questions i.e. we should check by dividing the value of $\angle A$ and $\angle B$ to see whether we get a ratio $3:2$ or not. So, dividing angle A by angle B, we get
$\dfrac{\angle A}{\angle B}=\dfrac{108}{72}=\dfrac{3}{2}$ . Thus, by doing this we can know that our answer is correct. Also, we can take any two adjacent angles i.e. $\angle A,\angle D$ or $\angle C,\angle D$ or $\angle C,\angle B$ for finding the answer. It is not necessary to take only $\angle A$ and $\angle B$ for solving the problem.