Question

The mass density of a spherical body is given by $\rho \left( r \right)=\dfrac{k}{r}$ for $r\le R$ and $\rho \left( r \right)=0$ for$r\rangle R$, where r is the distance from the centre. The correct graph that describes qualitatively the acceleration a of a test particle as function of r is:
A.

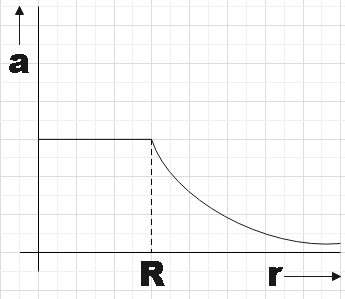
B.

C.
 

D.

Answer 1

Hint: You could first read the question and thus understand the situation properly. You could maybe find some relation that gives the dependency of acceleration of a test particle with distance as these are two parameters of which we are supposed to make a plot. Otherwise you could do it for parameters that have direct dependency on acceleration.
Formula used:
Electric force,
$F=qE$
Ampere’s circuital law,
$\int{E.dA=\dfrac{Q}{{{\varepsilon }_{0}}}}$

Complete answer:
We know that the electrostatic force could be given by,
$F=qE$
$\Rightarrow ma=qE$
So we could say that for a test particle of mass m and charge q, its acceleration would be directly proportional to electric field. That is,
$a\alpha E$ ………………………………………….. (1)
Now we could check the dependency of the electric field with distance r from the given conditions.
For $r\le R$ the mass density is given as,
$\rho \left( r \right)=\dfrac{k}{r}$
So we could say that charge contained within a sphere of radius r would be,
$Q=\int{\dfrac{k}{r}}dr\times 4\pi {{r}^{2}}=4k\pi \left( \dfrac{{{r}^{2}}}{2} \right)=2k\pi {{r}^{2}}$ ………………………………………… (2)
From ampere’s circuital we know that,
$\int{E.dA=\dfrac{Q}{{{\varepsilon }_{0}}}}$
$\Rightarrow E\left( 4\pi {{r}^{2}} \right)=\dfrac{Q}{{{\varepsilon }_{0}}}$
From (2),
$E=\dfrac{2k\pi {{r}^{2}}}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}=\dfrac{k}{2{{\varepsilon }_{0}}}$ ……………………………………. (3)
Therefore, we found that the electric field doesn’t depend on distance r and would be constant for $r\le R$ and so will be the acceleration of the test particle.
For $r\ge R,$ there is no dependency of mass density with distance, so,
$E=\dfrac{kQ}{{{r}^{2}}}$
So, we see that there is an inverse square dependence of the electric field with distance and so will the acceleration. So, we could say that if plot acceleration against distance the plot would look like the one in option A.

So option A is the correct answer.

Note: In questions like these where we are supposed to make a plot, we should take off the intervals that are taken into consideration. For example, here we have two intervals: one that is 0 to R and the region that is beyond R. We are also given necessary points for making the plot for the respective regions to make it easier.