Question

The magnitude of the electric field \[\overrightarrow{E}\] in the annular region of the charged cylindrical capacitor,
A) is the same throughout.
B) is higher near the outer cylinder than near the inner cylinder.
C) varies \[\dfrac{1}{r}\] as where r is the distance from the axis.
D) varies \[\dfrac{1}{{{r}^{2}}}\] as where r is the distance from the axis.

Answer 1

Hint: We can first draw a diagram of the annular region of the charged cylindrical capacitor. Then applying Gauss theorem on the region to find the magnitude of the electric field. The magnitude we get will tell us the dependence of the distance from the axis of the charged cylindrical capacitor.

Formula used:
\[\begin{align}
  & \phi =\dfrac{Q}{{{\varepsilon }_{0}}} \\
 & \phi =\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S
 E\cdot dA \\
\end{align}\]

Complete step by step answer:
The annular region for the charged cylindrical capacitor can be show as follows

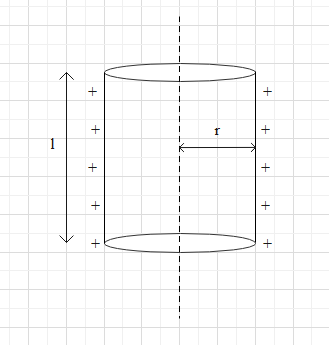
Where r is the distance from the axis and l is the length of the cylinder.
Now according to Gauss theorem, the electric flux is given as the ratio of charge enclosed within the closed surface to the permittivity in free space.
\[\phi =\dfrac{Q}{{{\varepsilon }_{0}}}\] …………. (i)
Where Q is the total charge enclosed in the closed surface and \[{{\varepsilon }_{0}}\]is the permittivity in free space.
In terms of the electric field it can be given as
\[\phi =\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S
 E\cdot dA \]
Where dA is the infinitesimal element of the area of the surface.
Now considering the above charged cylindrical capacitor, electric field will be constant and the integral of dA will be given as
\[\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S
 dA=2\pi rl \]
And the total flux become
\[\phi =E\left( 2\pi rl \right)\] …………. (ii)
The charged capacitor will have linear charge density, which can be given as
\[\lambda =\dfrac{Q}{l}\]
From this length can be given as \[l=\dfrac{Q}{\lambda }\]
Substituting value of l in equation (ii)
\[\phi =2\pi rE\left( \dfrac{Q}{\lambda } \right)\]
Now equating, equation (i) to (ii)
\[2\pi rE\left( \dfrac{Q}{\lambda } \right)=\dfrac{Q}{{{\varepsilon }_{0}}}\]
Now the electric field can be given as
\[E=\dfrac{\lambda }{2\pi {{\varepsilon }_{0}}r}\]
From this we can see that
\[E\propto \dfrac{1}{r}\]
Hence, the magnitude of electric field in the annular region of the charged capacitor varies by \[\dfrac{1}{r}\].

So, the correct answer is “Option C”.

Note: The magnitude of electric field for the point charge kept at distance r varies as \[\dfrac{1}{{{r}^{2}}}\] and therefore many can mistakenly say the correct option as D. But from the above derivation we can see that the magnitude of electric field is inversely proportional to the distance of the surface from its axis.